平方数列の和というのは
12+22+32+42+52+・・・・+n2
ガウスは小学生の時に1+2+3+・・・・nを求めたのでもうすこし難しい問題に挑戦！
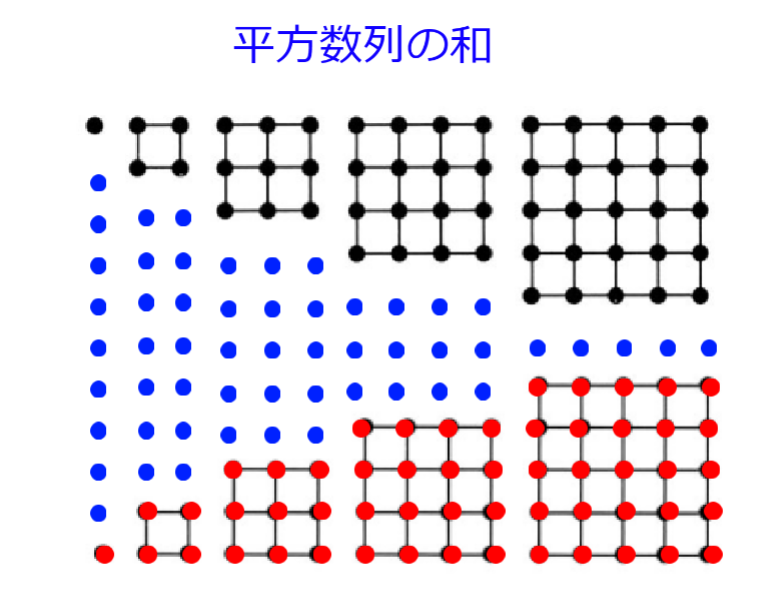
図はn=5のときに様子で赤丸の数が平方数列の和になる。
黒丸と青丸は同じ数の丸でこのように並べると長方形になる。
縦はn+2で横は1+2+3+・・・+nでガウスが求めた数
n(n+1)/2になる。
そこで平方数列の和はn(n+1)(n+2)/2÷3で求められる。
つまり平方数列の和
中村儀作・阿邊恵一著「代数を図形で解く」を参考にしました。
カテゴリー
平方数列の和を求める
「平方数列の和を求める」への2件の返信
この平方数列の和の求め方、図形によるものとしては之より簡単なもはないと言われる。果たしてそうか。義作先生も病気の中、これに挑戦しておられました。数の回転を含んだ方法を試されていました。1は1とっ、2は2っ、3は3つと、とぐろを巻くように数を足してゆく。すると、
5×6＝1+2×2+3×3+4×4
阿邊恵一様 コメントありがとうございます。
５０年前、中村儀作氏の講義を受けました。数学が苦手で講義内容はあまり理解できなかったのですが、素晴らしい講義をされ、とても楽しかったです。ずっと尊敬して、憧れています。
阿邊恵一様もきっと素晴らしい方なんでしょうね。