Haltyのホームページ

普通のやり方だと空白ができてしまう。

特に問題ないように見えるが．．．．　
次の動画も普通に埋め込む

つぎはリンクを張ってみる。https://youtu.be/NVUWQrgceXk
これの方がよいかも？

長針、短針、秒針のついた時計がある。7時から8時までの間で、短針と秒針の間の角度が120°になる23回目の時刻は7時何分何秒か？
面倒な問題です。短針と秒針の角度が120°になるのは1分間に2回あるので23回目は7時11分台の1回目。
7時11分ｘ秒の短針の角度は
\[210＋11×0.５＋\frac{x}{120}\]
秒針のｘ秒後の角度は6xなので
\[210＋11×0.５＋\frac{x}{120}-6x＝120\] となるxを求めればよい。
\[x=\frac{11460}{719}=15×\frac{675}{719}\]
答えは7時11分15.94秒

１から９９９までの整数のうち、約数の個数が5個であるものをすべて求めなさい。
難しい問題です。約数の個数が5個の整数は素数の４乗だということを知っていれば答えは分かります。
素数　　素数の４乗
２　　　２^４＝16
３　　　３^４＝27
５　　　５^４＝625
７　　　７^４＝2401
答えは16,27,625です。

それでは１から９９９までの整数のうち約数の個数が最も多い整数はいくらでしょう？
答え：８４０で約数の個数は32個

栄東中の入試問題
辺ABの中点をP、辺CDの中点をQとします。
PQの長さが6cmのとき、正四面体ABCDの体積は何㎠ですか。

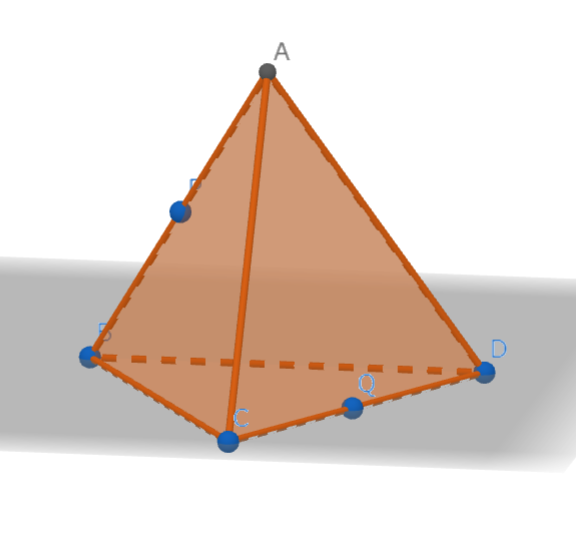
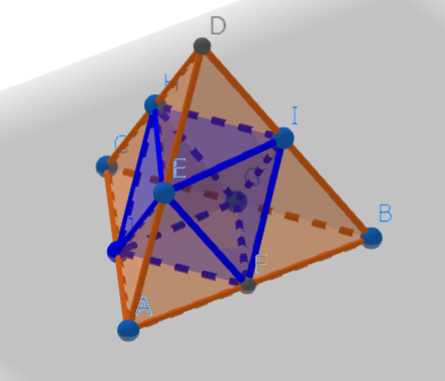
正四面体の各辺の中点を結ぶと正四面体の中に正八面体ができます。
この正八面体の体積を求めます。底面積は対角線の長さが5cmの正方形で高さが6cmなので６×６÷２×6÷3=36㎤です。正四面体の4隅に小さな正四面体が4個できます。小さな正四面体の体積を①とすると大きい正四面体の体積は⑧です。
⑧ー④は正八面体の体積になりますので⑧ー④＝④＝36㎤です。①=９となり小さい正四面体の体積が９㎠だと分かります。
大きい正四面体の体積は小さな正四面体の体積の8倍なので
９×８＝72㎤が答えです。

甲陽学院中の入試問題から

以下のように数が並んでいます。
1行目　1
2行目　3,4,5
3行目　7,8,9,10,11
4行目　13,14,15,16,17,18,19
5行目　21,22,23,24,25,26,27,28,29
　：
3600は何行目の何番目の数ですか？
各行の最初の数字は1,3,7,13,21,・・・
この数列の一般項 a_n=n²-n+1
n=60のときa₆₀=60²-60+1=3541
3600-3541+1=60
よって60行目の60番目

これも中学入試の問題です。四角形ABCDは正方形で三角形DEFは１辺の長さが８ｃｍの正三角形です。斜線部分の面積の合計は何㎠ですか。

これは難問です。解答を知るとちょっと感動するかも。
答えは16㎠です。

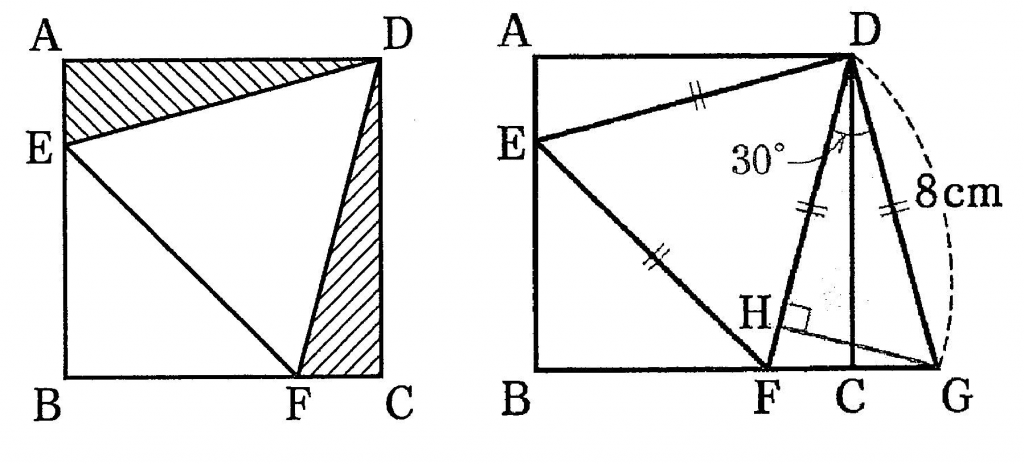
三角形DGHは30°、60°の角を持つ直角三角形だから
GH=DC÷2＝４(cm)
よって斜辺部分の面積の合計は
８×４÷２＝16（㎠）

中学入試の問題は本当に難しい！
ある池の周りをA君とB君は同じ方向に、C君は逆方向に、それぞれ一定の速さで回ります。A君はB君を15分ごとに追い越し、B君はC君と３分ごとに出会います。
B君が７分かかって回る距離をC君は８分で回ります。
A君とB君とC君の速さの比を求めなさい。［麻布中学校］

池の周囲の長さも分からないし、求めるのは速さの比です。小学生がこんな問題を解けるのでしょうか？
C君とD君は同じ距離を７分と８分で回るので速さの比は8:7です。B君とC君の速さを８と７にしましょう。
B君とC君は３分で出会うので
3×8+3×7=45 つまり池の周囲の長さが45です。
１５分間にA君が回る距離とC君の距離の差は池の周囲の長さになります。A君の速さをAとすれば
A×15-8×15=45
A×15=45+120=165
A=11
よってA:B:C=11:8:7