数列{an}のn項までの和がSn=n・3n+1-1で表されるときa1とn≧2に対する一般項anを求めよ。
a1=S1=9-1=8
an=Sn-Sn-1=n・3n+1-1-(n-1)3n=(3n-n+1)3n=(2n+1)3n
Sn=4n-anが成り立つとき
(1) 初項a1の値を求めよ。
S1=a1=4-a1 2a1=4 a1=2
(2) an+1をanで表せ。
an+1=Sn+1-Sn=4(n+1)-an+1-4n+an
an+1=an/2+2
(3) この数列の一般項を求めよ。
an+1-4=(an-4)/2 より{an-4}は初項がa1-4=2-4=-2,
公比が1/2の等比数列
an-4=-2×(1/2)n-1 より
an=-2×(1/2)n-1+4
a1=0, a2=3とし、
an+1=(4/3)an-(1/3)an-1 (n=2,3,4,・・・・)とする。
一般項を求めよ。
3(an+1-an)=an-an-1
(an+1-an)=(1/3)(an-an-1)
これは初項が3, 公比が(1/3)の階差数列なので
n-1
an=0+ Σ 3×(1/3)k-1 =(9/2)(1-31-n)
k=1
a1=1, an+1=(8an-1)/(25an-2) (n=1, 2, 3, 4,・・・)について以下の問いに答えよ。
(1) a2, a3, a4, a5を求めよ。
a1=1/2, a2=2/7, a3=3/12, a4=4/17, a5=5/22
分子はn, 分母は初項2, 公差5の等差数列と予想する。
an=n/{2+5(n-1)}=n/(5n-3)
このanをan+1=(8an-1)/(25an-2)に代入する
分子は(8an-1)=(8n-5n+3)/(5n-3)=(3n+3)/(5n-3)
分母は(25n-10+6)/(5n-3)=(15n+6)/(5n-3)
よってan+1=(3n+3)/(15n+6)=(n+1)/(5n+2)………①
また、an=n/(5n-3)より
an+1=(n+1)/{5(n+1)-3}=(n+1)/(5n+2)………②
①=②から予想は正しい。
a1=1, an+2an=4・(-2)n (n=1,2,3,・・・)で定まる数列{an}について、次の問いに答えよ。
(1) a2, a3, a4を求めよ。
(2) bn=an/(-2)nとするとき、{bn}のみたす漸化式を求めよ。
(3) anをnの式で表せ。

(1)は計算して求めればよい。
(2)はとりあえずb1, b2, b3, b4を求めてみると初項が-0.5, 公差が-2の等差数列だと分かる。漸化式はbn=bn-1-2
bn=-0.5-2(n-1)=-2n+1.5
an=(-2n+1.5)×(-2)n
MITに面白い時計が設置されたと聞きました。
Kendall/MITという地下鉄の駅前に設置されているそうです。
時計の文字盤が回転します。
この情報と動画を送ってくれたMITの和田一実教授に感謝します。
早速このような時計をプログラムで作ってみました。プログラム言語はMITの時計ということでScratchを使いました。
スタートボタンを押すと時計が動き始めます。また、猫にタッチすると通常の時計になります。
MITでなぜこのような時計を設置したのでしょう?
普通の時計は文字盤は固定されていて時計の針だけが回転している。でも文字盤も回転する。これは天動説から地動説の変わるコペルニクスの転換を暗示しているのではないか! といった友達がいます。
MITの時計は奥の深い時計です。
数学の問題をプログラムで解く
n2/250, n3/256, n4/243 がすべて整数となるような正の整数nのうち、最小のものを求めよ。
この問題はプログラムを使うと一瞬でもとめることができる。
—————————————
n=1
while(n*n % 250 + n**3 % 256 + n**4 % 243>0):
n+=1
print(n)
—————————————
答えはn=1800
ネットでこのような問題が紹介されていました。
x14+x7+1を係数が実数の範囲で因数分解せよ。
簡単そうに見えます。しかし、これは数学検定1級の問題でしかも解答が間違っていたという有名な難問だそうです。
日本の数学は因数分解の勉強にすごく時間をかけていると言われていますが、確かにそうだと思います。
実際に解いてみました。
とりあえずf(x)=x14+x7+1がどんなグラフになるのかを見てみましょう。グラフはパソコンやスマホで簡単に表示できます。
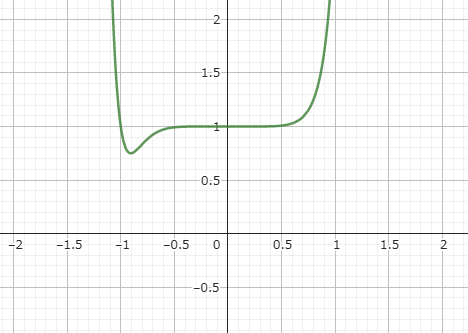
x軸とは交わらないのでf(x)=0となるxは虚数になることが分かります。つまり因数定理なんかでは因数分解できない。
それならx7=Xとすればこの式はX2+X+1になります。
X2+X+1=0となるXは解の公式よりX=(-2±i√(3))/2
この値をxとしてf(x)に代入するとf((-2±i√(3))/2)=0となることからf(x)は(x2+x+1)で因数分解できることが分かります。
早速 (x14+x7+1)÷(x2+x+1)を筆算で計算すると
f(x)=(x2+x+1)(x12-x11+x9-x8+x6-x4+x3-x+1)
これでとりあえず因数分解できました。
「係数が整数の範囲で因数分解せよ」というのならこれで正解です。
しかし「係数が実数の範囲で因数分解せよ」というのだからさらにこれは因数分解できます。
2次方程式でよく出てくる完全平方は面倒なのでメモとして公式を紹介します。
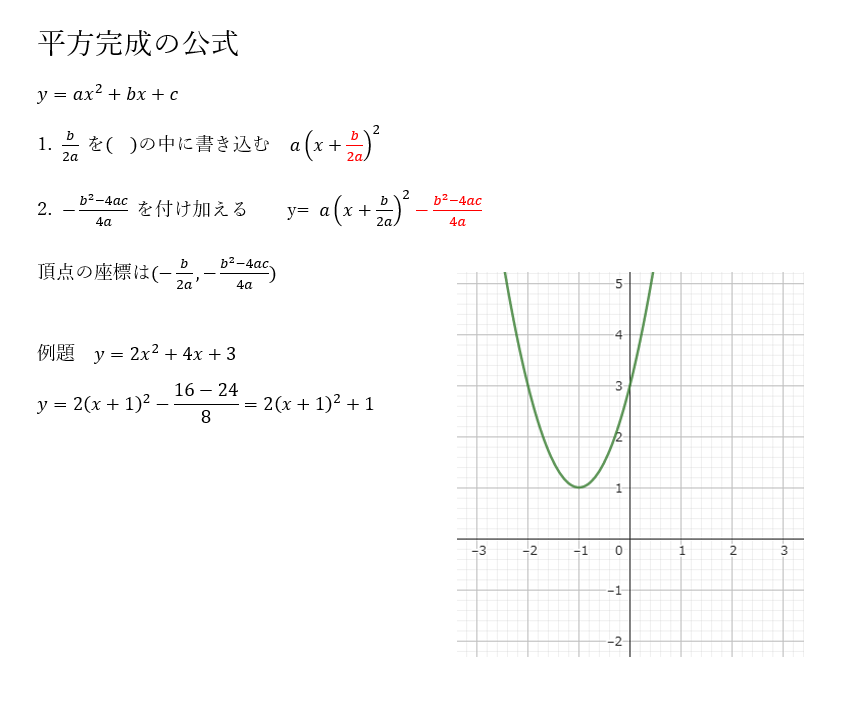
5円玉で月の大きさを測る
満月の時、腕を伸ばして5円玉の穴から月をのぞくと5円玉の穴に月がおさまります。ぴったりおさまったときの目と5円玉の距離は55cm、5円玉の穴の大きさは5mm、月までの距離は約38.5万kmなので計算で月の直径を求めることができます。
月の直径は3474kmなのでほぼ正確に求められました。
