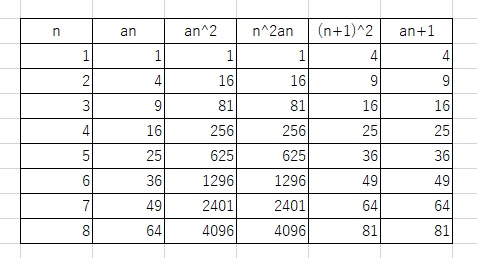
ｎとanを値を眺めながら推定する。
an=n2と仮定する。n=1のときa1=1なので成り立つ。
ak=k２とすると
ak+1=ak2-k2ak+(k+1)2
=k4-k4+(k+1)2=(k+1)2 となりk+1のときにも成立する。以上からan=n2という推定は正しい。
カテゴリー
漸化式 推定→帰納法
（1）a1=3, an+1=-an+2
c=-c+2よりc=1
an+1-1=-(an-1)
bn=an-1とすると
bn+1=-bn
b1=a1-1=3-1=2よりbnは初項２で公比-1の等比数列である。
bn=2(-1)n-1
an-1=2(-1)n-1 より an=2(-1)n-1+1
(2) a1=2, 2an+1-3an=3
2c-3c=3 より c=-3
an+1+3=3/2(an+3)
bn+1=3/2bn
b1=a1+3=5 よりbnは初項5で公比3/2の等比数列である。
bn=5(3/2)n-1
an+3=bnよりbn=5(3/2)n-1-3
カテゴリー
図形の簡単そうな問題
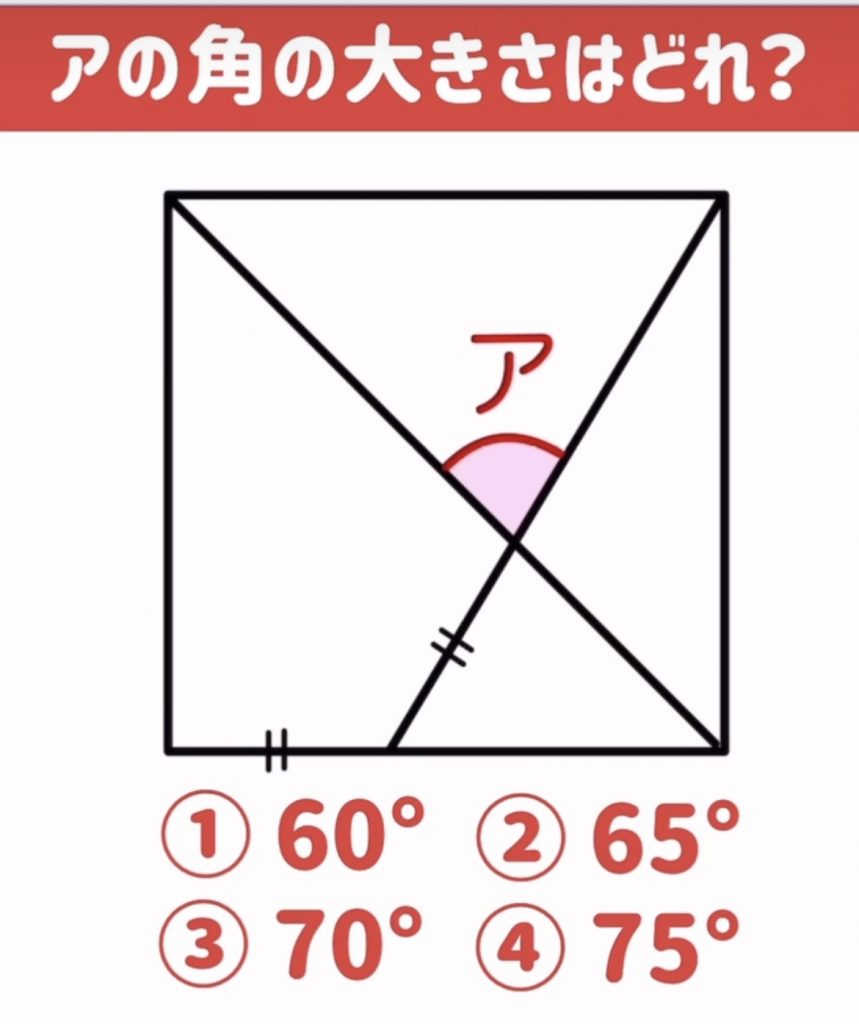
簡単に解けそうな問題である。しかしよく分からない。長さが等しいという線分の長さを求めてみる。
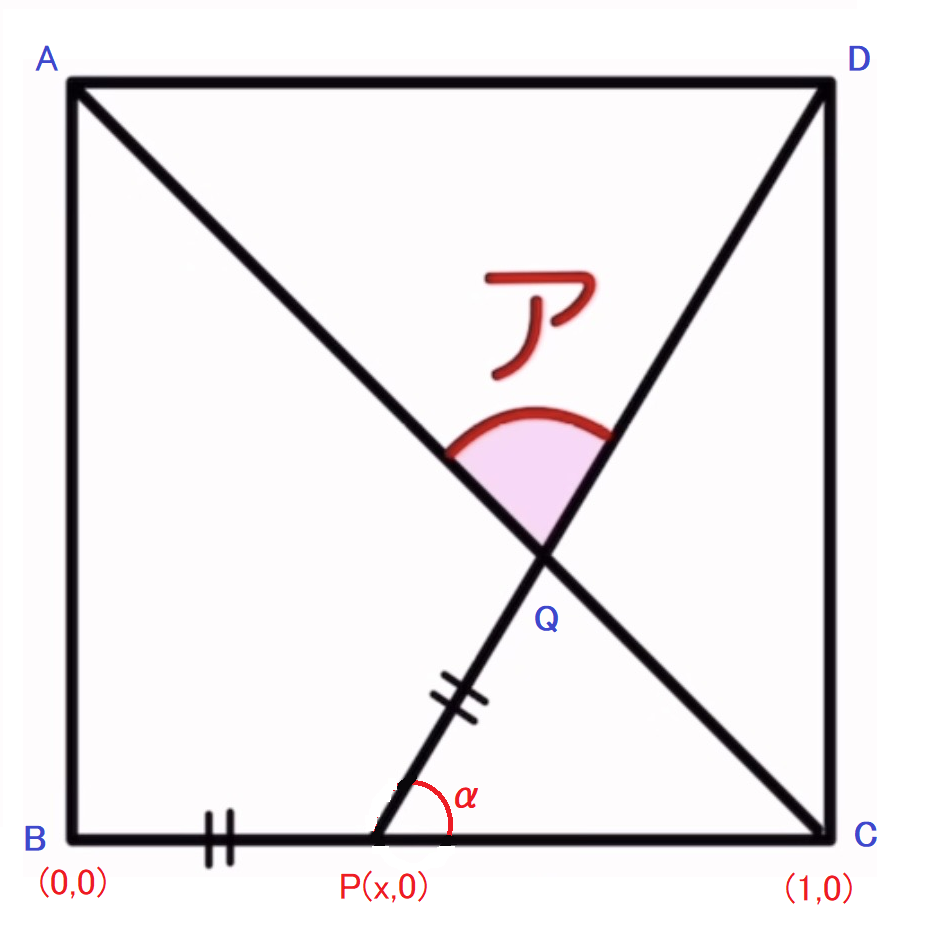
点Pと直線y=-x+1の距離がｘに等しいという式からｘを求める。x=(1-x)/√(2) よりx=√(2) – 1
tan α = 1/PC=1/(2-2√2) より α ≒59.6388
αはほぼ60°になる。
ア≒180-45-60＝75となる。
4択問題なので④を選ぶことになるが正確な値ではない。
これからLINEを始める人のための手順を説明します。
LINEは日本の人口の約70％が利用いるコミュニケーションツールです。
手順１ LINEをダウンロードしてインストールする
スマホにインストールします。iPhoneはAppStoreからダウンロードします。Androidは Google Playからダウンロードしてください。
LINEでアプリを検索するとこのようなものが出てきますのでインストールしてください。
スマホの画面に緑のLINEのアイコンが表示されればインストール完了です。
手順２ 新規登録をする
LINEを起動したら最初に新規登録をします。これが面倒です。このページを参考にしてください。
https://guide.line.me/ja/signup-and-migration/line-signup.html
ここに書かれている「友達追加設定」では友達自動追加と友達への追加を許可のチェックを外しておくことをお勧めします。
新規登録はうまくできましたでしょうか？
もしうまくいできなかった方はコメントをください。
オンラインミーティングに参加するには
オンラインミーティングに参加するためのURLがメールで届きます。このURLにスマホのブラウザでアクセスすれば「LINEアプリで開いて続行してください。」という画面がでるので
「LINEアプリを開く」を選んでください。
オンラインミーティングはパソコンでやりたいと思うかも知れません。パソコンにLINEをインストールするにはこちらを参照してください。
https://guide.line.me/ja/services/pc-line.html
LINE友達になろう
友達になろうと言ってQRコードを見せられることがあります。その人とLINE友達になる方法を紹介します。
まず、スマホでLINEを起動します。
次に左下のホームアイコンにタッチします。
次に右上の友達追加アイコンにタッチします。
すると友達追加の画面に変わるのでQRコードを選びます。
するとカメラ画面になるので友達が表示しているＱＲコードにカメラを向けます。カメラが友達を認識したらタッチしましょう！
それでは実際にやってみましょう。うまく友達になれましたか？
算数オリンピック2007 ファイナル問題7
水平な床に長さ2007cm、奥行2cm、高さ2cmの直方体の箱があり、その中を半径1cmの球が転がるようになっています。
箱の丁度中央には球Cがあり、その左に球A、右に球Bがそれぞれ接しています。3つの球の半径は全て1cmです。
いま、球Aが左向きに毎秒7cm、球Bが毎秒37cmの速さで同時に転がり始めました。球Cは静止したままです。
この後、はじめて3つの球が同時に衝するまでの間に球Cは何cmの道のりを転がるか？
ただし各球は何もないところでは等しい速度で真っ直ぐ進み、壁にぶつかると反射して同じ速さで逆向きに進み、球と球が衝突するとそれぞれの速度と向きが相手の球の速度と向きに入れ替わることが知られています。
問題を読むだけでも疲れてしまいます。これは難問です。
これを小学生が解くのは大変です。とりあえず、いつものようにプログラミングで解いてみました。緑のスタートボタンを押してください。
球C（ピンクのボール）が22回の正面衝突をしてその移動距離が22011cmだと分かります。プログラムはこのように球の動作をシミュレートするのは得意です。Scrathはスプライトの衝突を検知するのでプログラムが簡単にできます。さて、この問題を小学生がプログラムも使わずどのように解けばよいのでしょう。
ピンクのボールの動きだけに注目しましょう。規則正しく移動していることが分かります。
長さ2007cmを移動しますが球の半径がすべて1cmです。3つの球の直径を引いてやれば点A,B,Cが移動することになり計算が略になります。
つまり長さを2007-２×３＝2001cmと考えます。ここを点Cが移動する様子をみれば小学生でも移動距離を計算できます。
ネコにタッチすれば求め方を解説してくれます。
数学おもしろセンス 関根章道著（技術評論社）より
x3y-xy3-x2+y2-2xy-1 を因数分解せよ。
ヒント：2xyをxy+xyと分解して考えてみましょう
x2y2+x3y-x2-(x2y2+xy3+xy)+y2–xy
ここでx2y2と-x2y2を挿入します。すると以下のように変形できます。こんなの思いつかないよう！
=x2(y2+xy-1)-xy(xy+y2-1)+(y2+xy-1)
=(x2-xy+1)(y2+xy-1)
みごとに因数分解できました。
カテゴリー
累乗が入った漸化式
a1=1, an+1=3an – 2n という漸化式を解け。
累乗が入った漸化式はknを掛けたり割ったりすることで単純な漸化式になることが多い。
両辺を2n+1で割ると
an+1/2n+1 = 3an/(2・2n) – 1/2
ここでbn=an/2nとおくと、
bn+1 = 3bn/2 – 1/2
2bn+1 = 3bn – 1
bn = -(3/2)n/3+1
an = 2nbn = 2n – 3n-1
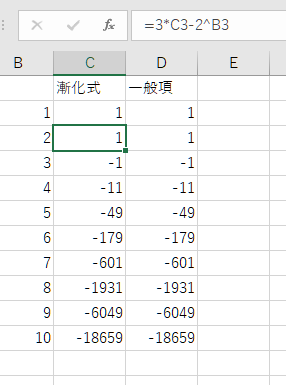
漸化式から一般項を求めるのはとても難しい。
しかし、実際こんな必要があるのだろうか？
コンピュータを使えば漸化式から簡単に値を求めることができる。
Excelで計算した例であるが、セルC1にa1の値を入れてc2に漸化式の式 [=3*C3-2^B3]を入れて下にコピーするだけで計算できる。
どんな難しい漸化式でも大丈夫。
これで良いのではないか？
a1=1,an+1-an=n(n+1)で定義される数列{an}について
a20とS20を求めよ。
an=1+1・2+2・3+・・・・+n(n+1)
an=1+Σ[k=1..n-1]k2+Σ[k=1..n-1]k
=1+(n-1)n(2n-1)/6+n(n-1)/2
=(n3-n+3)/3+1
a20=2661
Sn=(Σ[k=1..n]k3 – Σ[k=1..n]k + 3n)/3
=[{n(n+1)/2}2 – n(n+1)/2 +3n]/3
=n(n3+2n2-n+10)/12
S20=14650
数列{an}は、a1=1/2, a2=2, an+1×an-1=(an)2 (n≧2)を満たしている。このときanを求めよ。
an+1/an=an/an-1より等比数列だと分かる。
a1=1/2、a2/a1=4よりanは初項1/2,公比4の等比数列なのでan=1/2×4n-1
カテゴリー
正方形の面積を求める
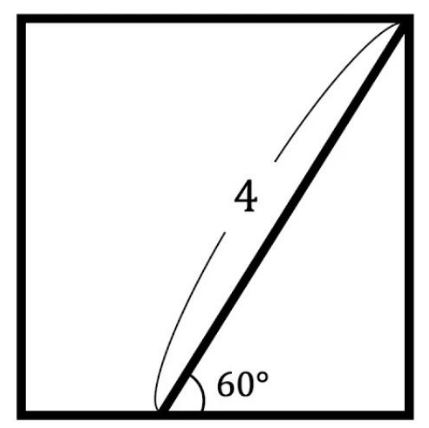
中学生以上なら三平方の定理や三角関数を使って一瞬で解く問題かもわかりませんが、これは小学生の問題です。なので三平方の定理や三角関数は使ってはいけません。
この問題を紹介して解答したホームページについて多くのコメントが付いていました。多かったのがECの長さを２として解いている時点で三平方を使っているのではないかというものでした。
また解き方もとても難しくて小学生には無理だという意見が多かったようです。ただ、この図形を4個並べて4倍の正方形の面積を求めるという方法は面白いと感じました。
とりあえず小学生でも解けそうな方法を私なりに考えてみました。
まず、三平方の定理を使わなくてもEC＝２になることを証明しましょう。
三角形CDFは2等辺三角形。
三角形CEFは正三角形なの各辺DF, EF,CF,CEの長さはすべて等しく２になります。
CQは正三角形CEFの垂線なので辺EFを2等分します。だから辺EQの長さは１です。QDの長さは４－１＝３です。
三角形DPCの面積は４×３÷２＝６です。
この三角形の面積は正方形の面積の半分なので正方形の面積は６×２＝１２です。