簡単にとく裏技を紹介していますが、普通の解いたらどのようになるかを紹介します。そうしないとここでやった解き方がどんなに凄いか分ってもらえないと考えたからです。
共通テスト2022 数Ⅱ・B 問3(3)です。


別の解き方もあります。
全く図は意識せず長さが√6になる t を求める方法です。

これだとOQの長さが√6になるtは2つしかないことも分かります。

パソコンを使えば瞬時に解は求まります。
簡単にとく裏技を紹介していますが、普通の解いたらどのようになるかを紹介します。そうしないとここでやった解き方がどんなに凄いか分ってもらえないと考えたからです。
共通テスト2022 数Ⅱ・B 問3(3)です。


別の解き方もあります。
全く図は意識せず長さが√6になる t を求める方法です。

これだとOQの長さが√6になるtは2つしかないことも分かります。

パソコンを使えば瞬時に解は求まります。
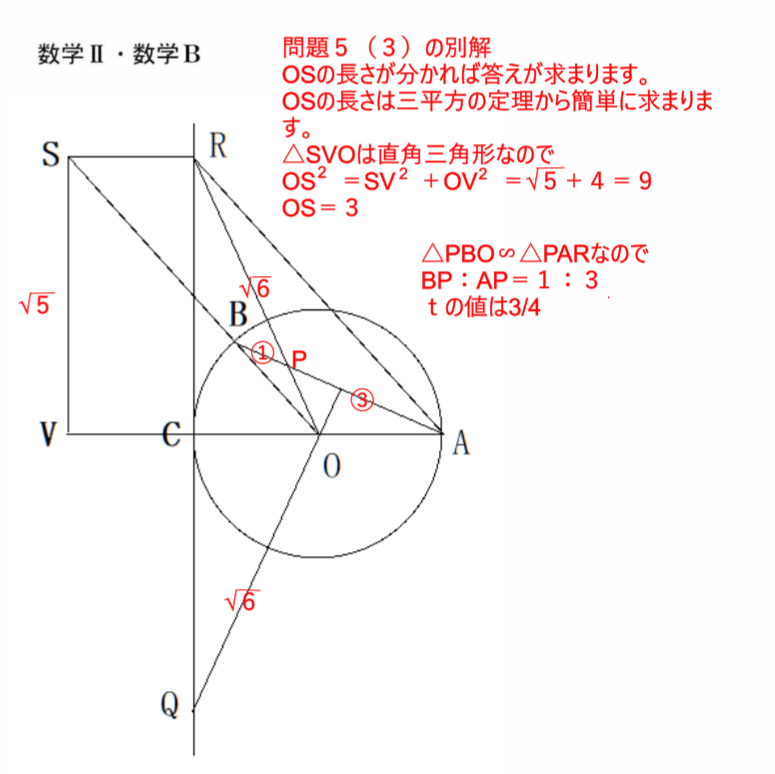
2022年共通テスト数Ⅱ・B 問題5(3)
難しい計算で解いている人が多いが、図形の問題として解けば簡単です。
3平方の定理だけであっという間に答えが求まります。
2022数Ⅱ・B 第4問(2)
自転車が歩行者に追いついたら1分どちらも休憩してまた歩行者は歩き始める。自転車は家に戻って1分休憩してからまた歩行者を追いかける。
4回目に自転車が歩行者に追いつく時刻を求めます。
旅人算はプログラムでダイアログを描けば簡単に求めることができます。
プログラムを見たら分かりますが137分が答えです。
このダイアログを見たら、定規があれば簡単に描けることが分かります。計算するよりずっと簡単です。
2022年の数Ⅱ・Bの問題から 第4問(1)
旅人算の問題で歩行者を自転車で追いかける問題です。
(1)の数列は簡単に求められますが、その一般項を求めるのは難しいです。しかし、共通テストはマークシート形式なので解答群があります。

この中から正解を選べば良いのです。
数列の値は分かっているので解答群のnに1, 2, 3を代入して値を求めます。
an=2,8,24・・・ bn=2,7,22 となるものを選びます。
anは⑨でbn=は⑦が正解です。超簡単!!
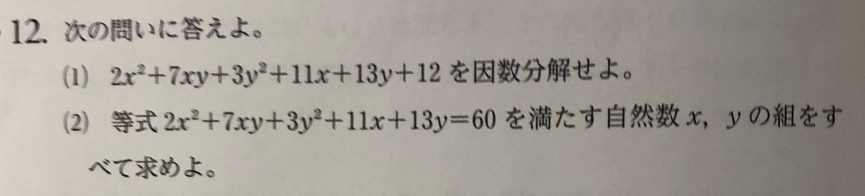
Pythonで解きました。
import math
for x in range(1,100):
for y in range(1,100):
if 2x*x+7x*y+3y*y+11*x+13*y==60:
print(x,y)
x=2,y=1

これをPythonで解くと次のようになる。
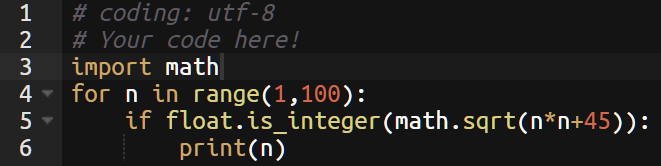
結果は2,6,22となる。
まず、平方根の計算をするのでmathをインポートする。
nを1~100までで平方根が整数になるものを見つけている。
ちょっと考えればnは45より大きくないことが分かるが、適当に大きい値を選べばよい。このプログラムでは100以下だろうと予測した。
不安ならもっとでっかい数字にすればよい。
真面目な解き方
√(n^2+45)=mとおいて
n^2+45=m^2
m^2-n^2=45
(m+n)(m-n)=45
(m+n,m-n)=(45,1),(15,3),(9,5)の3種類
m+n=45,m-n=1のとき、m=23,n=22
m+n=15,m-n=3のとき、m=9,n=6
m+n=9,m-n=5のとき、m=7,n=2
答え、n=2,6,22
VARDIA D-B1005Kというレコーダーを使っていたのですが、テレビ番組の録画に失敗するようになりHDDの書き込みに失敗したとかHDDにキズがあり修復できないとかのメッセージが出たり起動もしなくなりました。

ネットで検索するとレコーダーのトラブルの記事がいっぱいありこの機種の修理の動画もありました。
10分で簡単にHDDの交換できるという動画がありました。HDDを交換することをHDD換装というそうです。
左右2個、後ろの3個のレジをドライバーで外すと簡単にケースを空けることができました。
中にHDDが入っています。4個のネジで簡単に外せました。SUMSUNGのSERIAL ATA でした。

SAMSUNGの1TバイトのHDD
同等のHDDがネットで3~4千円程度で売られているので購入しようかと思ったのですが、先日、古くなったノートパソコンを廃棄するときに取り外したSDDがあることを思い出しました。

SDDメモリー
HDDよりコンパクトなので換装も簡単です。
問題なく認識できたので初期化して再起動起動してみると問題なく立ち上がりました。
動作確認ということでいくつかのテレビ番組を録画してみましたがすべて順調です。
これで修理完了! 分かりやすい動画を掲載してくれた皆さんに感謝です。

山頂の仰角を求める問題
問題は三角関数表を使って解くがプログラムを使えば簡単に求められる。
中学生がこのような問題を解いていました。
分数40/41を少数で表したとき、小数第99位の数字を求めよ。
循環小数を利用して求める問題ですが、面倒なので指定した桁まで割り算をするプログラムを作ってみました。
このプログラムを使えばどんな問題も一瞬で解けます。

循環小数表示をする関数電卓もあります。

中学3年生に問題の解き方を尋ねられた。
その問題は「4人でじゃんけんをするときあいこになるパターンは何通りあるか?」というものであった。とりあえず、真面目に数学的に解くことにした。
あいこになる場合は
ぐう、ぐう、ちょき、ぱあ
ぐう、ちょき、ちょき、ぱあ
ぐう、ちょき、ぱあ、ぱあ の3通りである。
ぐうが2個、ちょき、ぱあがそれぞれ1個ずつの組合せは
4C2✕2=6✕2=12通りある。
同様に他の2つの場合も12通りなので12✕3=36通り が答え!
簡単な問題である。
これをプログラムで解いてみよう。
シラミつぶし法でじゃんけんのすべてのパターンをつくってその中からあいこのものだけをカウントする。
Pythonだと
i=1
for w in (‘a’,’b’,’c’):
for x in (‘a’,’b’,’c’):
for y in (‘a’,’b’,’c’):
for z in (‘a’,’b’,’c’):
s= w+x+y+z
if (‘a’ in s) and (‘b’ in s) and (‘c’ in s):
print(i,’:’,s)
i=i+1
出力結果は
1 : aabc
2 : aacb
: abac
: abbc
35 : ccab
36 : ccba
となり36通りであることが分かる。
Scratchで同じようなプログラムを作ると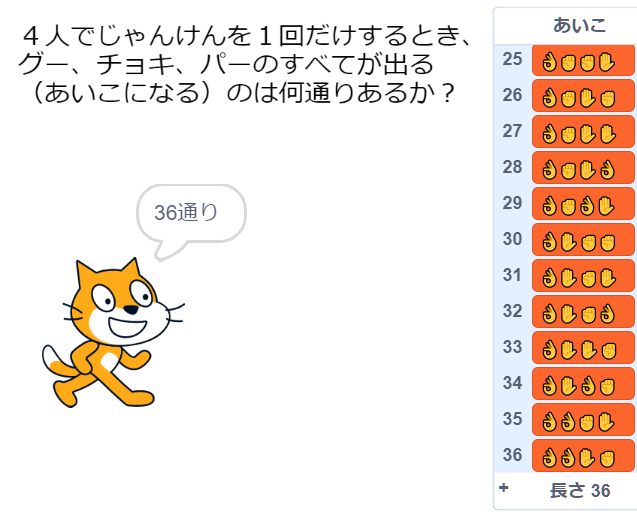
これも簡単にできる。
しかし、気分を変えてこの問題をモンテカルロ法で解いてみた。
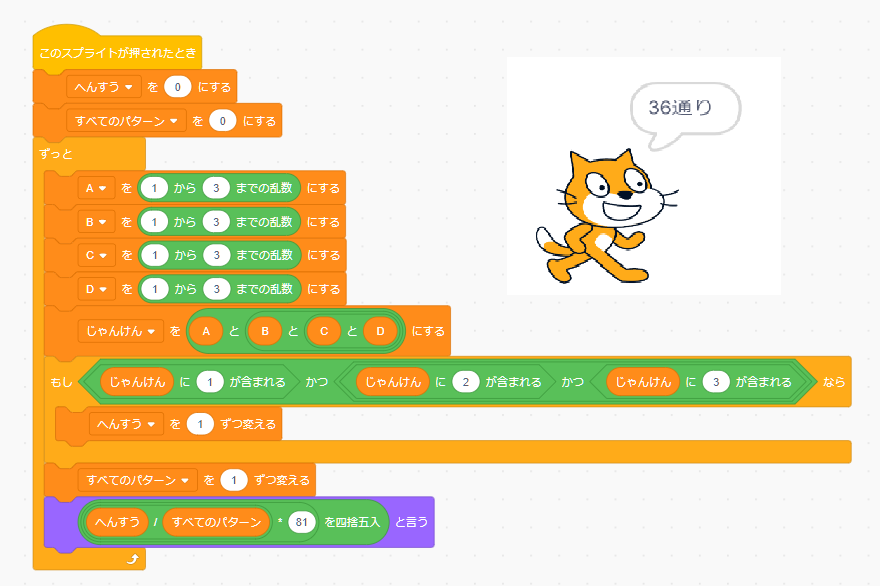
4個の変数をぐう、ちょき、ぱあの乱数にしてあいこだったらカウントするというやり方で求めてみた。
すぐに36通りに収束した。これはモンテカルロ法のよい使用例になったかも。