右の図のように、1辺の長さが8cmの立方体がを3個組み合わせた立体があります。この立体を3点A,B,Cを通る平面で切断したとき、切口の図形の面積は何㎠ですか。
東京都市大付属中学校の入試問題より

三角形ABCがこのように配置できることに気づけば簡単です。12×12の正方形から周囲の三角形の面積を引けば求められます。

右の図のように、1辺の長さが8cmの立方体がを3個組み合わせた立体があります。この立体を3点A,B,Cを通る平面で切断したとき、切口の図形の面積は何㎠ですか。
東京都市大付属中学校の入試問題より

三角形ABCがこのように配置できることに気づけば簡単です。12×12の正方形から周囲の三角形の面積を引けば求められます。
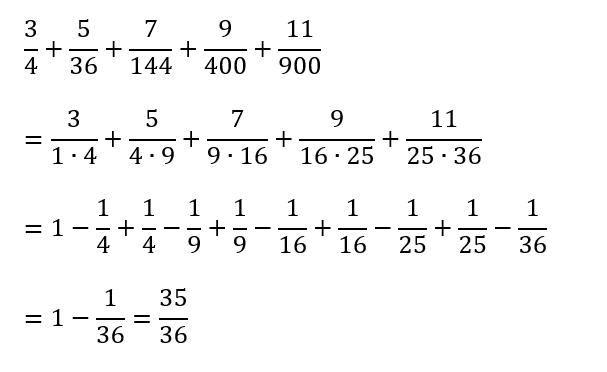
城北埼玉中の問題から
分数の問題を見たら部分分数分解を使って解くのが定番らしい
実際にプログラムで一筆書きをさせましょう。
ここをクリックするとプログラムの画面が開きます。
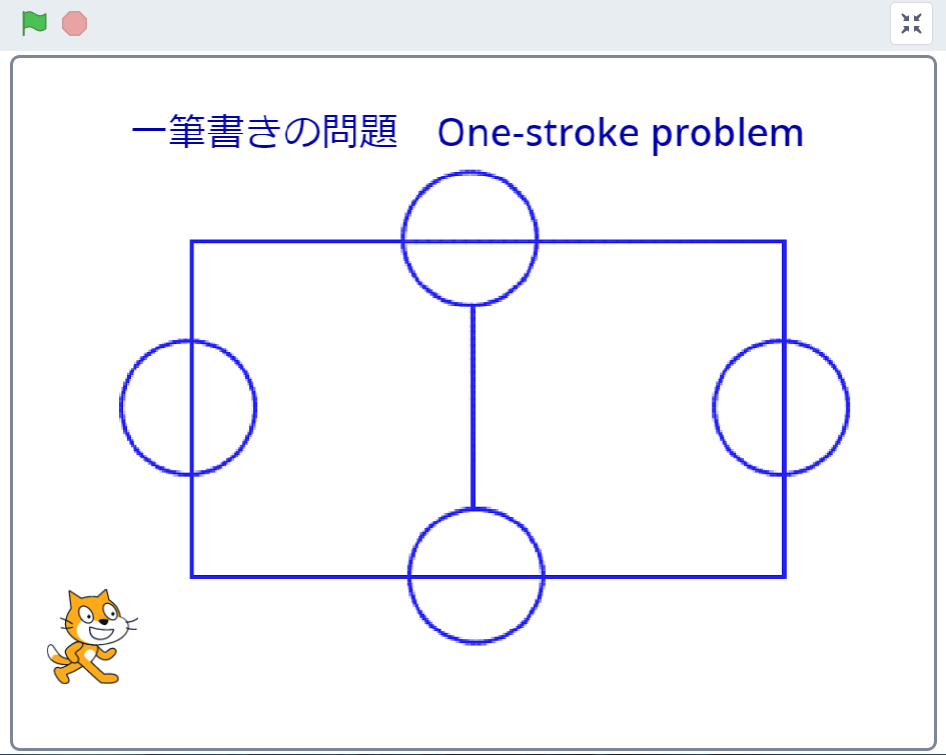
孫が暇そうにしていたので一筆書きの問題を出しました。
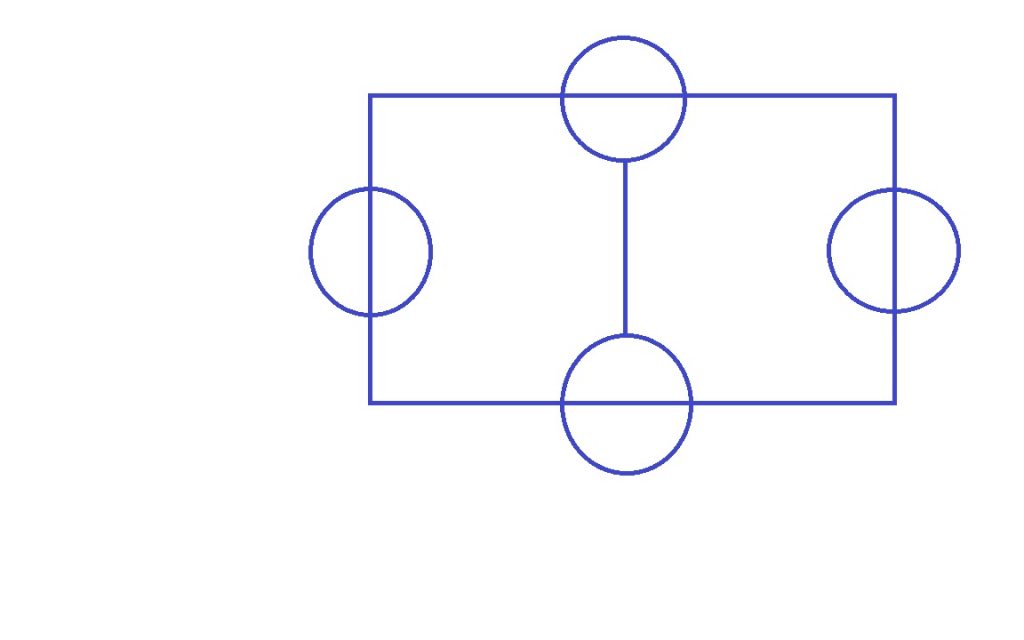
この図を一筆書き
苦労していましたが無事に一筆書きができました。皆さんも挑戦してください。
学生時代グラフ理論の講義で習ったような。
もう昔の話ですがこの図が一筆書きできるかどうかは分かります。これはできます。
それではこれはどうでしょう?
ケーニヒスベルクの七つの橋問題と呼ばれる有名な問題を分かりやすくしました。
ケーニヒスベルクの七つの橋問題
有名な問題を分かりやすくしたものです。
この図は残念ながら一筆書きできません。
共通テスト2022 数学Ⅰ・数学A 第4問 (4)
114を24で割ったときの余りは1に等しい。不定方程式
115x-25y = 1
の整数解のうち、xが正の整数で最小になるのは
x=【テト】、y=【ナニヌネノ】
である。
数学的に不定方程式の問題を解くのはなかなか難しいのですがプログラミングを使えば一瞬で解けます。
Pythonのプログラム
————————————
for x in range(10,100):
for y in range(90000,100000):
if(11**5-2**5*y==1):
print(‘x=’,x,’ y=’,y)
————————————-
x= 19 y= 95624
この難問も5行のプログラムで解けます。
次の□に入る数字を二項定理を用いて求めよ。
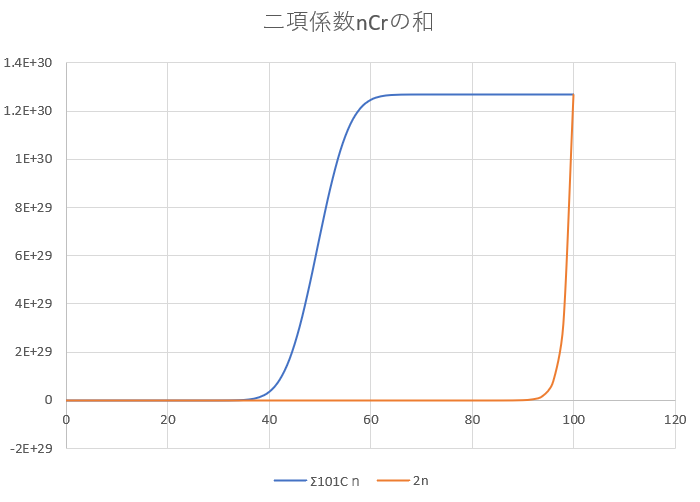
101C0 + 101C2 + 101C4 + …+101C98 + 101C100=2□
この問題を解いているホームページがありました。
エレガントな解法です。
私はExcelで解いてみました。グラフ表示をすれば100だと分かりました。
沖田神社でひょうたん石を見て感動していたら、幸島稲荷神社(水門町715)にもひょうたん石があるというのでここにも行ってみました。この神社は山の上にあり、見晴らしがすばらしいです。でも道が狭くて運転は緊張しました。こちらの石垣にはひょうたんのほかに桃と盃もありました。河内屋治兵衛という人が作ったのではないかと言われているようです。

こちらにはひょうたん石だけでなく桃石、盃石もありました。みごとな技術です。他のところで見かけないことからかなり難しい技巧だと思います。
ネットで検索すると大分の八幡朝見神社の敷石にひょうたんや盃の石があると紹介されていました。

天気も良く暖かかったので沖田神社に行きました。
スタンプラリーの台紙があったのでこれから15個のスタンプを集めようと思います。締め切りは9月30日です。対象の神社で一番近いのがこの神社でした。

大鳥居
立派な神社です。駐車場も広くて自動車でも行きやすい場所です。

ひょうたん石
気になっていたのがこれです。
沖田神社の本殿の土台に「ひょうたん形」の石が組み込まれて、これが治兵衛の仕業ではないか、言われています。
幸島稲荷神社にも本殿土台にも同じような石が組み込まれているとか。
ここにも行ってみようと思います。