令和5年度 本試験の正解
数Ⅰ・A 本試験の正解
数Ⅱ・B 本試験の正解
令和5年度 追・再試験の正解
令和5年度 数Ⅰ・A 追・再試験の正解
令和5年度 数Ⅱ・B 追・再試験の正解
共通テストの自己採点ツール
共通テストの過去問題
カテゴリー: 共通テスト
Scratchで共通テスト 数学Ⅰ・A 数学Ⅱ・Bの自己採点アプリを作りました。
共通テスト過去問題自己採点
2020河合塾共通テスト模試自己採点
共通テストの学習ツール
共通テストの解答を入力すると採点してくれるホームページやツールはいろいろあるのですが、学習にはあまり効率が良くないことに気づき自作してみました。
共通テストの数学の問題は決まった解き方に従って解いていき、最終的に答えが求まるという流れなので途中で間違うとそれ以降の答えがすべて誤りという悲惨な結果になります。
このプログラムは間違うと正解するまで何度でも聞き直され、先に進めないのです。
ただそれだけのことですが、実際に使ってみると効果は抜群でした。
ここをクリックしてご利用ください。
不定方程式を解く
共通テスト2022 数学Ⅰ・数学A 第4問 (4)
114を24で割ったときの余りは1に等しい。不定方程式
115x-25y = 1
の整数解のうち、xが正の整数で最小になるのは
x=【テト】、y=【ナニヌネノ】
である。
数学的に不定方程式の問題を解くのはなかなか難しいのですがプログラミングを使えば一瞬で解けます。
Pythonのプログラム
————————————
for x in range(10,100):
for y in range(90000,100000):
if(11**5-2**5*y==1):
print(‘x=’,x,’ y=’,y)
————————————-
x= 19 y= 95624
この難問も5行のプログラムで解けます。
共通テストの問題を普通に解いたら
簡単にとく裏技を紹介していますが、普通の解いたらどのようになるかを紹介します。そうしないとここでやった解き方がどんなに凄いか分ってもらえないと考えたからです。
共通テスト2022 数Ⅱ・B 問3(3)です。


別の解き方もあります。
全く図は意識せず長さが√6になる t を求める方法です。

これだとOQの長さが√6になるtは2つしかないことも分かります。

パソコンを使えば瞬時に解は求まります。
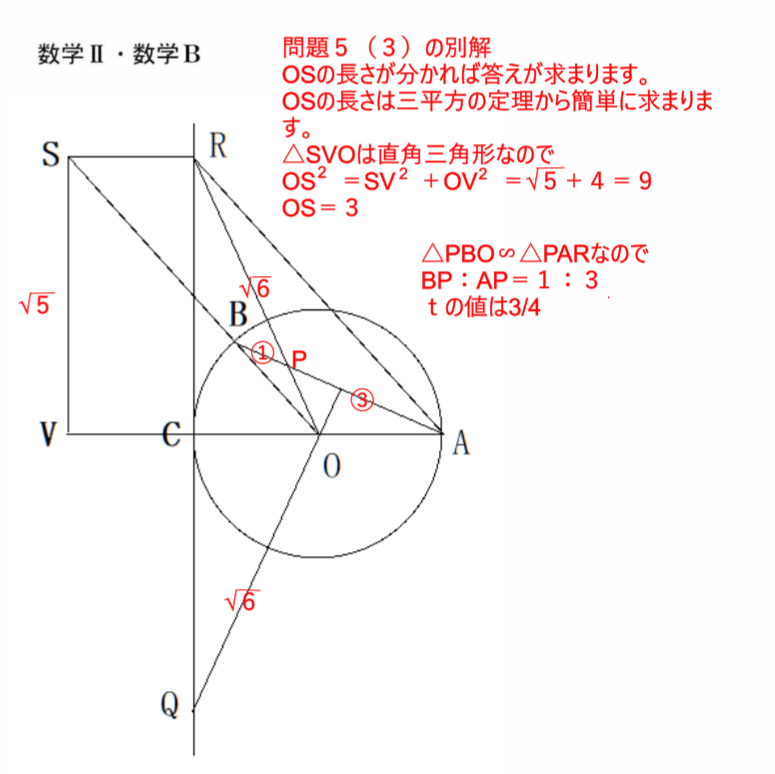
共通テストの問題を超簡単に解く裏技(3)
2022年共通テスト数Ⅱ・B 問題5(3)
難しい計算で解いている人が多いが、図形の問題として解けば簡単です。
3平方の定理だけであっという間に答えが求まります。
共通テストを超簡単に解く裏技2
2022数Ⅱ・B 第4問(2)
自転車が歩行者に追いついたら1分どちらも休憩してまた歩行者は歩き始める。自転車は家に戻って1分休憩してからまた歩行者を追いかける。
4回目に自転車が歩行者に追いつく時刻を求めます。
旅人算はプログラムでダイアログを描けば簡単に求めることができます。
プログラムを見たら分かりますが137分が答えです。
このダイアログを見たら、定規があれば簡単に描けることが分かります。計算するよりずっと簡単です。
共通テストを超簡単に解く裏技!
2022年の数Ⅱ・Bの問題から 第4問(1)
旅人算の問題で歩行者を自転車で追いかける問題です。
(1)の数列は簡単に求められますが、その一般項を求めるのは難しいです。しかし、共通テストはマークシート形式なので解答群があります。

この中から正解を選べば良いのです。
数列の値は分かっているので解答群のnに1, 2, 3を代入して値を求めます。
an=2,8,24・・・ bn=2,7,22 となるものを選びます。
anは⑨でbn=は⑦が正解です。超簡単!!
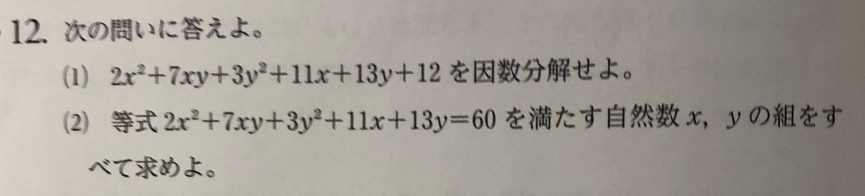
Pythonで解きました。
import math
for x in range(1,100):
for y in range(1,100):
if 2x*x+7x*y+3y*y+11*x+13*y==60:
print(x,y)
x=2,y=1

これをPythonで解くと次のようになる。
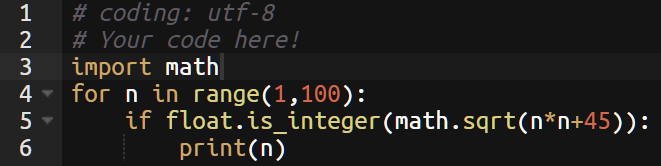
結果は2,6,22となる。
まず、平方根の計算をするのでmathをインポートする。
nを1~100までで平方根が整数になるものを見つけている。
ちょっと考えればnは45より大きくないことが分かるが、適当に大きい値を選べばよい。このプログラムでは100以下だろうと予測した。
不安ならもっとでっかい数字にすればよい。
真面目な解き方
√(n^2+45)=mとおいて
n^2+45=m^2
m^2-n^2=45
(m+n)(m-n)=45
(m+n,m-n)=(45,1),(15,3),(9,5)の3種類
m+n=45,m-n=1のとき、m=23,n=22
m+n=15,m-n=3のとき、m=9,n=6
m+n=9,m-n=5のとき、m=7,n=2
答え、n=2,6,22