平方数列の和というのは
12+22+32+42+52+・・・・+n2
ガウスは小学生の時に1+2+3+・・・・nを求めたのでもうすこし難しい問題に挑戦!
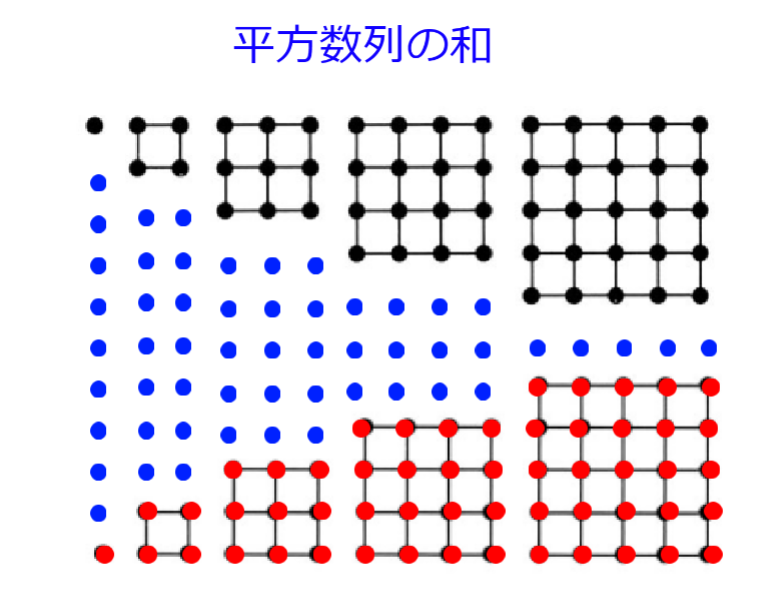
図はn=5のときに様子で赤丸の数が平方数列の和になる。
黒丸と青丸は同じ数の丸でこのように並べると長方形になる。
縦はn+2で横は1+2+3+・・・+nでガウスが求めた数
n(n+1)/2になる。
そこで平方数列の和はn(n+1)(n+2)/2÷3で求められる。
つまり平方数列の和
中村儀作・阿邊恵一著「代数を図形で解く」を参考にしました。
平方数列の和というのは
12+22+32+42+52+・・・・+n2
ガウスは小学生の時に1+2+3+・・・・nを求めたのでもうすこし難しい問題に挑戦!

図はn=5のときに様子で赤丸の数が平方数列の和になる。
黒丸と青丸は同じ数の丸でこのように並べると長方形になる。
縦はn+2で横は1+2+3+・・・+nでガウスが求めた数
n(n+1)/2になる。
そこで平方数列の和はn(n+1)(n+2)/2÷3で求められる。
つまり平方数列の和
中村儀作・阿邊恵一著「代数を図形で解く」を参考にしました。
Fn=22^n+1 (nは自然数, 2^nは2n)
F0=3
F1=5
F2=17
F3=257
F4=65537
F0からF4はすべて素数です。
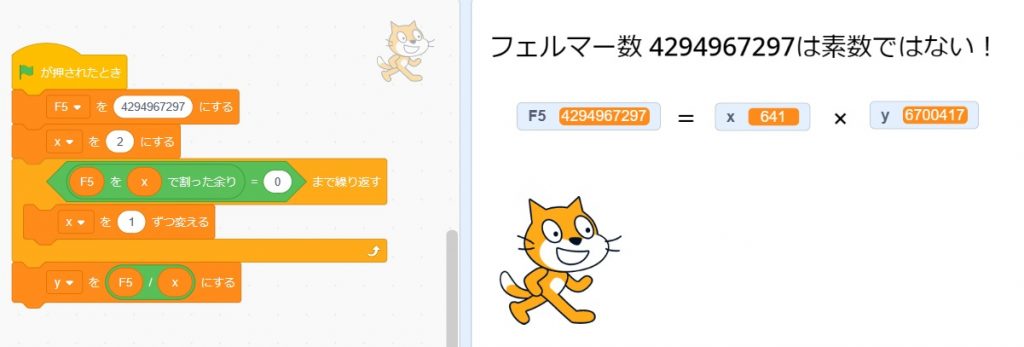
フェルマーはF5=4294967297も素数だろうと予想しました。フェルマーから約百年後、1732年にオイラーはフェルマーの予想が誤りであったことを示しました。
F5が素数でないことは簡単に示せます。
F6はScratchでは難しいのでPythonで解きました。
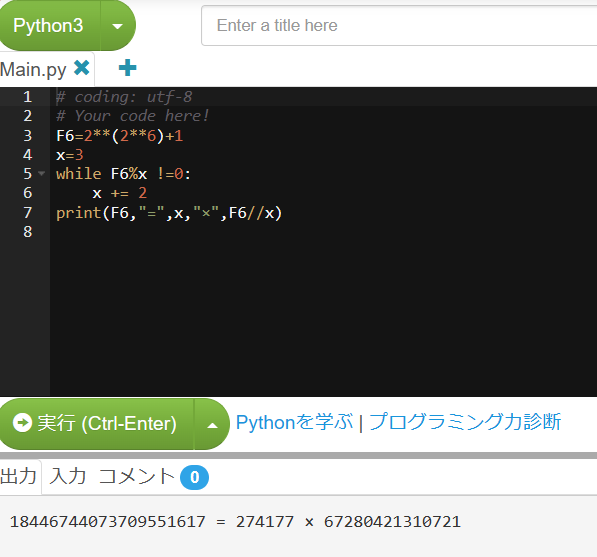
Pythonだと簡単に素因数分解できました。これでF6は素数でないことが分かります。
フェルマーの予想から百年後にオイラーがF5が誤りであることを示しましたがそれから150年近くたった1880年にランドリーによって素因数分解されました。驚くことに80歳を過ぎてからの大発見だったそうです。
その後コンピュータを使ってF7,F8,F11が素因数分解できることが解き明かされています。
この記事は「面白くて眠れなくなる数学」桜井進著を参考にしました。
余談ですが、F7の値が初版では間違っていました。
私立の高校入試の問題はどんどん難しくなっている。
理大付属高校の入試問題にこのようなものがありました。
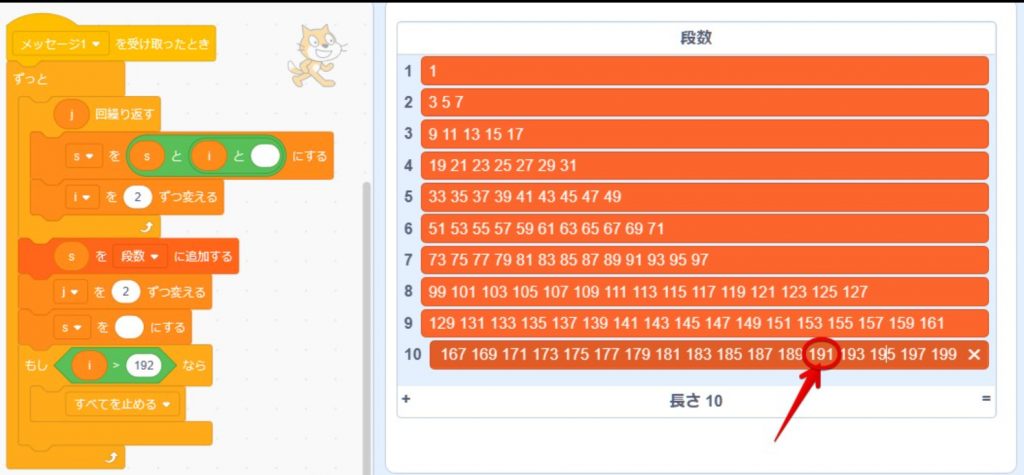
問題 図のように奇数を順番に規則的に並べていくと191は何段目の右から何番目にあるか?
1段 1
2段 3 5 7
3段 9 11 13 15 17
4段 19 21 ・ ・ ・ ・ ・
解答 右から何番目からというので各段の右端の数字を並べてみると 1,7,17,31,・・・と続く。高校生だとこれは階差数列だと分かり、一般項を求める。→ 2n2-1
これが191を超えるのはn=10の時で10段の右端が199だと分る。
10段 ・・・191,193,195,197,199
よって答えは10段の右端から5番目だと分かる。
しかし、受験生が階差数列を解けるとは思えない。どやって解くことを出題者は期待しているのだろう。
プログラムを使えば簡単に解くことができる。
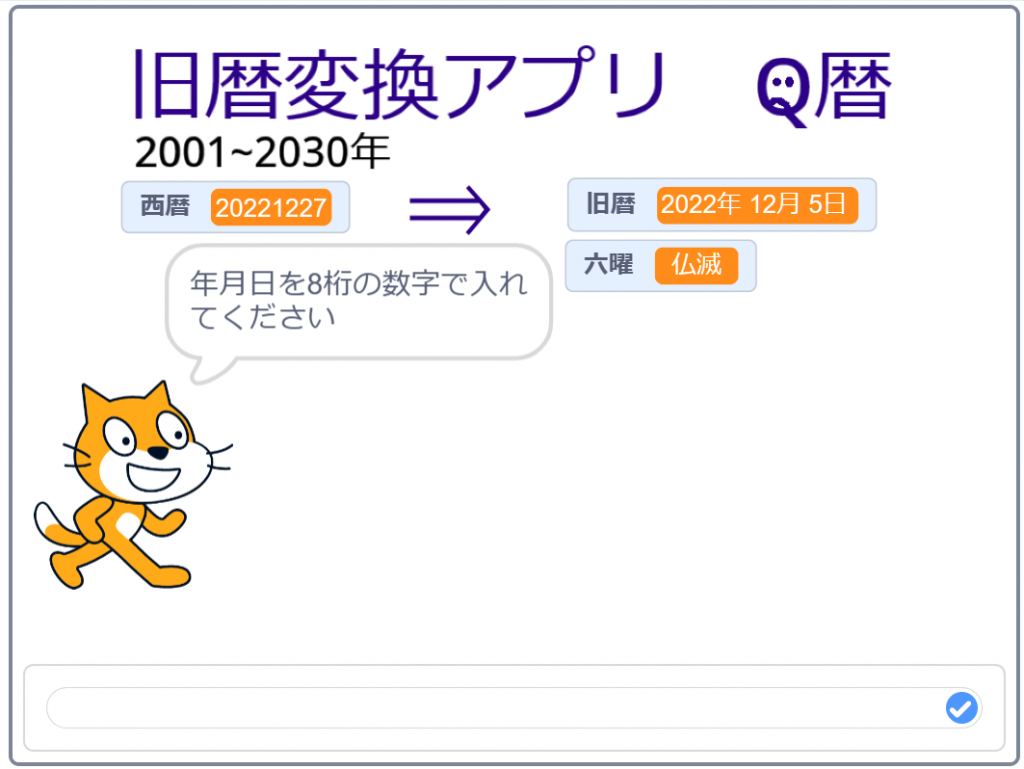
40年も前に旧暦に変換するアプリを作りました。まだOSはMS-DOSでパソコンはPC-9801です。
図書館で旧暦に関する本を見つけて読んでいると意外と簡単にできることが分かり早速作ってみました。
そのアプリの名前はQ暦でパソコン通信のネット(まだインターネットは無い)にフリーソフトとして掲載しました。
六曜が表示されるので「結婚式に日取りを決めるのにご利用ください」とコメントを付けました。
翌日、多くの方からコメントをもらいアプリのダウンロード数がどんどん増えていました。
こんなに多くの人が結婚するのかと驚いたんですが、実は建築関係の人がダウンロードしていました。棟上げは大安にするのですが、年々も先の日程が分からなくて困っていたそうです。
それから医療関係の人です。大安に退院したりするそうで勤務表を作るときに助かるそうです。
こんなに人気になるならフリーソフトではなく有料にすればよかったと後悔しました。
当時のことを思い出しながらQ暦の復刻版を作りました。懐かしいです。
和算にはパズルのような楽しい問題があります。
1斗桶の中に1斗(10升)の油が入っている。この油を7升桝(マス)と3升桝を使って5升と5升に分けなさい。
これは面白いので早速プログラムしてみました。


本に書かれていたパズルは「ただし、橋は川に垂直にかけるものとする」と追加されている。
これはよく見かけるパズルで橋の幅についてはなにも書かれていないので幅の広い大きい橋を適当にかければそれで解答になる。
しかし、手元の本の解答を見ると以下のような条件を追加すべきだと思う。
「橋は長方形で渡るには中央をまっすぐ進むこととする。」と追加すればよいだろう。
さて、この問題を解いてもらいたい。
私はいつものようにScratchで答えを求めた。
橋の位置を変えながら距離を測定して最短距離となる橋の位置を求めるプログラムを作った。
もちろんプログラムを使わなくても簡単に橋をかける位置を見つけることができる。
Scratchで共通テスト 数学Ⅰ・A 数学Ⅱ・Bの自己採点アプリを作りました。
共通テスト過去問題自己採点
2020河合塾共通テスト模試自己採点