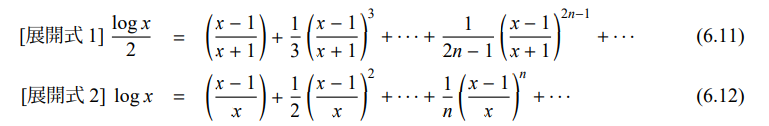問題 4を4つと四則演算を使って0~9をつくりなさい。
図書館で借りた本に掲載されていた問題です。
とりあえず、解いてみました。と言ってもプログラムを作りましたが。
4□4□4□4 の四角に+-×÷のいずれかが入る
0=4÷4×4-4
1=4÷4+4-4
2=4÷4+4÷4
3=?
4=?
5=?
6=?
7=4+4-4÷4
8=4+4+4-4
9=4÷4+4+4
3~6が解けない。解答を見ると括弧を使ってる!
プログラムを作り直す。
3=(4+4+4)÷4
4=(4-4)÷4+4
5=(4×4+4)÷4
6=(4+4)÷4+4
ちなみに10はできません。プログラムではすべてのパターンを検証したのでできないことが分かります。
やはり小町算の方が美しい!
カテゴリー: 未分類
73×77も暗算で瞬時に解ける!
7×(7+1)=56 で3×7=21 なので5621
最初にこの計算法を知ったときは凄いと感動した。
ただし、この計算法が使えるのは2桁の数字の10のくらいの数字が同じで1のくらいの2つの数字を足すと10になる場合に限られる。この条件を満たす掛け算のパターンは81通り。
全ての掛け算のパターンは81×81=6561通りなのでランダムに2桁の数字の問題が出るときにこの条件を満たす掛け算の問題で出る確率は100問の問題に1問程度である。
これでは寂しい! もう1つの計算法も覚えよう。
1のくらいの数字が同じで10のくらいの2つの数字を足すと10になる場合も同じような計算法になる。
47×67は4×6+7=31で7×7=49となり3149
これも美しい! この2つの計算法を知っていれば100問の問題の中に2問程度はこの方法が使える問題がある。
大切なもの(高学年の部 合唱)
シンクロBOM-BA-YE(高学年の部 合奏)
ともだち いいね(低学年の部 歌)
聖者の行進(低学年の部 合奏)
チャレンジ!(中学年の部 歌)
銀河鉄道999(中学年の部 合奏)
数学の問題をプログラムで解く
n2/250, n3/256, n4/243 がすべて整数となるような正の整数nのうち、最小のものを求めよ。
この問題はプログラムを使うと一瞬でもとめることができる。
—————————————
n=1
while(n*n % 250 + n**3 % 256 + n**4 % 243>0):
n+=1
print(n)
—————————————
答えはn=1800
ここで埋め込むと便利なことがあるのかな?
サンプルとして以前作ったものを使ってみます。教え子が作ったプログラムのプレゼンをした時のものです。
懐かしい!
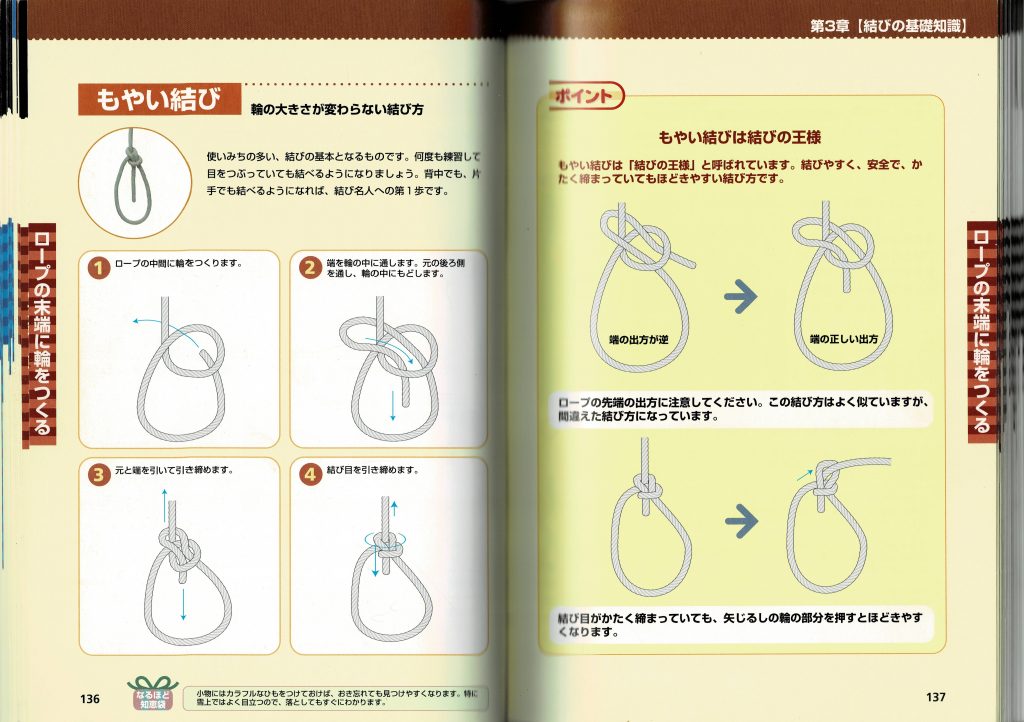
もやい結びは結びの王様だそうです。
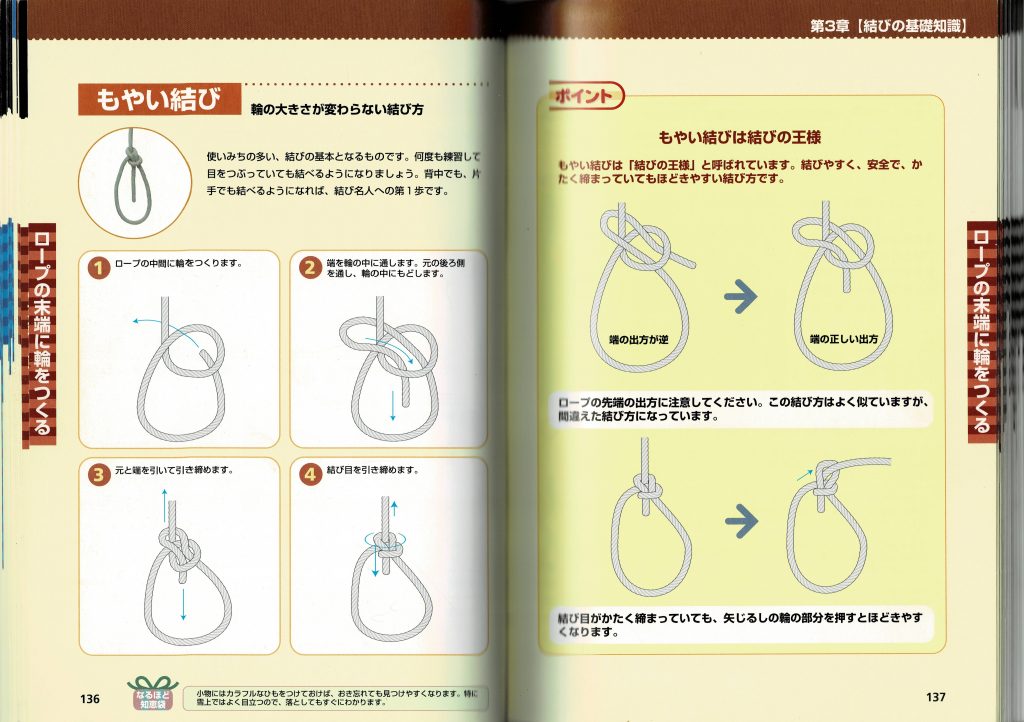
Youtubeの埋め込み
普通のやり方だと空白ができてしまう。
特に問題ないように見えるが....
次の動画も普通に埋め込む
つぎはリンクを張ってみる。https://youtu.be/NVUWQrgceXk
これの方がよいかも?
長針、短針、秒針のついた時計がある。7時から8時までの間で、短針と秒針の間の角度が120°になる23回目の時刻は7時何分何秒か?
面倒な問題です。短針と秒針の角度が120°になるのは1分間に2回あるので23回目は7時11分台の1回目。
7時11分x秒の短針の角度は
\[210+11×0.5+\frac{x}{120}\]
秒針のx秒後の角度は6xなので
\[210+11×0.5+\frac{x}{120}-6x=120\] となるxを求めればよい。
\[x=\frac{11460}{719}=15×\frac{675}{719}\]
答えは7時11分15.94秒
HTMLを簡単に埋め込むことができることが分かった。
これは便利だと思う。