数学検定の5級、準2級の合格を目指している人のために練習アプリを作りました。
しっかり練習して合格することを祈っています。
カテゴリー: 数学
数学の問題をプログラムで
500以下の自然数のうち、正の約数が15個である数の個数と求めよ。
for i in range(1,501):
k=0
for j in range(1,i+1):
if i % j ==0:
k=k+1
if k==15:
print(i)
——————————
144
324
400
答えは3個です。プログラムを使えばこんなに簡単に解けます。
しかしきっと数学の先生は怒るから真面目に解きましょう。
積が15になる自然数の組み合わせは1×15と3×5です。
よって約数が15個である数を素因数分解すると
p1-1q15-1=q14またはp3-1q5-1=p2q4の形です。
ただしp,qは素数でp≠q
q14≦500 またはp2q4≦500となるp,qを求めましょう。
q14≦500となるqはありません。
prime=[2,3,5,7,11]
for p in prime:
for q in prime:
if p**2*q**4<=500 and p!=q:
print(p,q,p**2*q**4)
——————————————
2 3 324
3 2 144
5 2 400
高校生の問題集にこんな問題がありました。
1から100までの100個の自然数の積
N=1・2・3・………・100 を計算すると、末尾には0が連続して何個並ぶか。
スマホの電卓でも100!は簡単に求められる。
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000000
答えは24個です。つまらない問題!
しかしスマホで答えたのでは数学としての問題の意味がないので真面目に解答しましょう。
5が約数の数字と2が約数の数字をかけると末尾に0が付きます。2が約数の数字は50個もあるので5が約数の数だけ0が付くと考えます。100÷5=20なので0は末尾に20個連続します。これが正解かと思うとそうではありません。約数5が2個の数字もあるからです。つまり約数に25がある数字はさらに0の数が増えます。100÷25=4なので0の数は20+4=24個連続することになります。
約数5が3個ある数字も考えましょう。これは53=125になり100を超えてしまうのでありません。
以上のことから答えは24個になります。
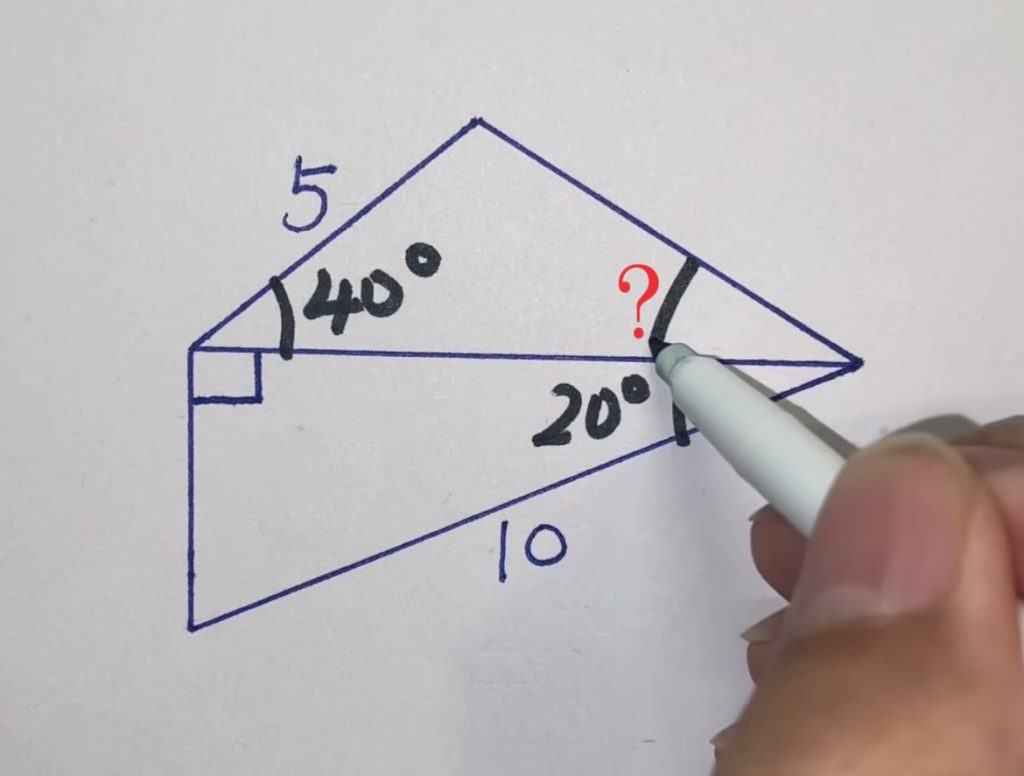
2辺の長さとその間の角度が分かっていれば三角形の残りの値が分かるのでそれを利用しようと思う。きっともっと簡単な方法があると思うけど思いつかない。
2辺は5と10Cos20°でその間の角度が40°なので残った辺の長さをxとすると
x2=52+(10Cos20°)2-2・5・(10Cos20°)Cos40°
Sin?=5・Sin40/x=0.5
よって?=30°

2024年ということで2024に関連した問題を作ってみようと思いました。実はこのような問題をネットで見つけました。
a!-b2+4c=2024を満たす自然数(a,b,c)を全て求めよ
これは面白い問題だと思ったのですが、答えは解なしです。
やはり解がある問題の方が楽しいと思い作りました。
—————————————–
2a-b3-4c=2024を満たす自然数(a,b,c)を求めよ
解答はコメント欄に!
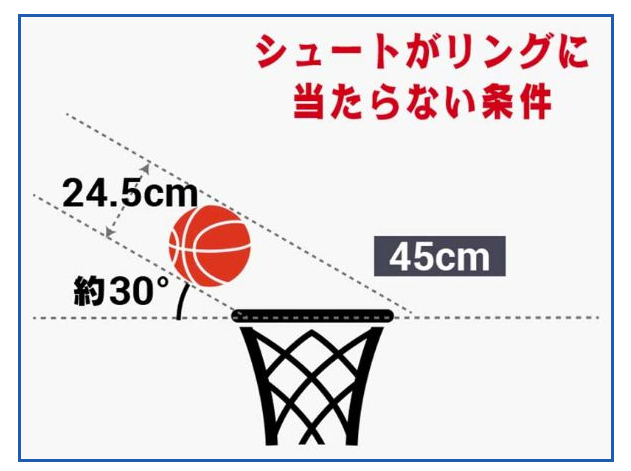
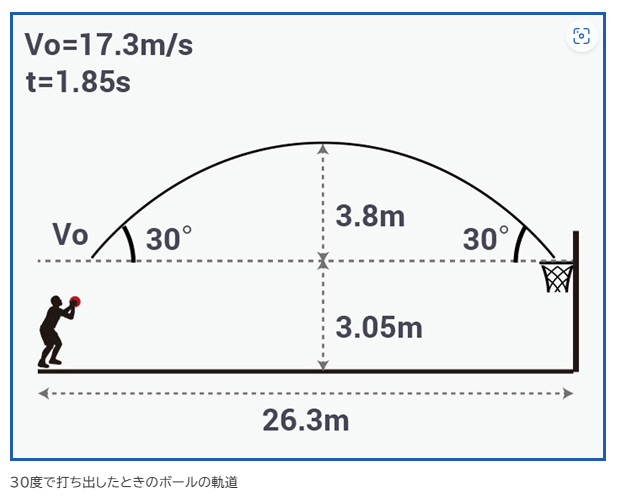
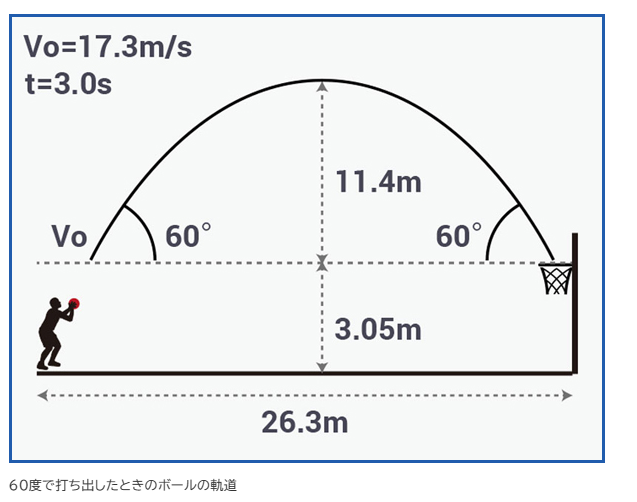
バスケットボールの問題
漸化式 推定→帰納法
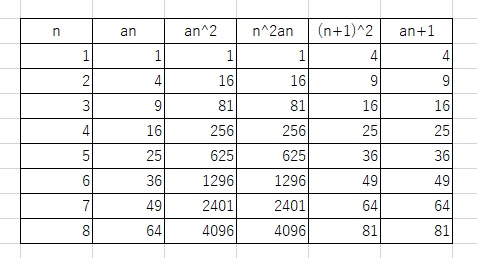
nとanを値を眺めながら推定する。
an=n2と仮定する。n=1のときa1=1なので成り立つ。
ak=k2とすると
ak+1=ak2-k2ak+(k+1)2
=k4-k4+(k+1)2=(k+1)2 となりk+1のときにも成立する。以上からan=n2という推定は正しい。
(1)a1=3, an+1=-an+2
c=-c+2よりc=1
an+1-1=-(an-1)
bn=an-1とすると
bn+1=-bn
b1=a1-1=3-1=2よりbnは初項2で公比-1の等比数列である。
bn=2(-1)n-1
an-1=2(-1)n-1 より an=2(-1)n-1+1
(2) a1=2, 2an+1-3an=3
2c-3c=3 より c=-3
an+1+3=3/2(an+3)
bn+1=3/2bn
b1=a1+3=5 よりbnは初項5で公比3/2の等比数列である。
bn=5(3/2)n-1
an+3=bnよりbn=5(3/2)n-1-3
数学おもしろセンス 関根章道著(技術評論社)より
x3y-xy3-x2+y2-2xy-1 を因数分解せよ。
ヒント:2xyをxy+xyと分解して考えてみましょう
x2y2+x3y-x2-(x2y2+xy3+xy)+y2–xy
ここでx2y2と-x2y2を挿入します。すると以下のように変形できます。こんなの思いつかないよう!
=x2(y2+xy-1)-xy(xy+y2-1)+(y2+xy-1)
=(x2-xy+1)(y2+xy-1)
みごとに因数分解できました。
累乗が入った漸化式
a1=1, an+1=3an – 2n という漸化式を解け。
累乗が入った漸化式はknを掛けたり割ったりすることで単純な漸化式になることが多い。
両辺を2n+1で割ると
an+1/2n+1 = 3an/(2・2n) – 1/2
ここでbn=an/2nとおくと、
bn+1 = 3bn/2 – 1/2
2bn+1 = 3bn – 1
bn = -(3/2)n/3+1
an = 2nbn = 2n – 3n-1
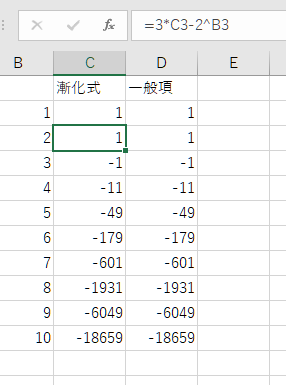
漸化式から一般項を求めるのはとても難しい。
しかし、実際こんな必要があるのだろうか?
コンピュータを使えば漸化式から簡単に値を求めることができる。
Excelで計算した例であるが、セルC1にa1の値を入れてc2に漸化式の式 [=3*C3-2^B3]を入れて下にコピーするだけで計算できる。
どんな難しい漸化式でも大丈夫。
これで良いのではないか?