□×□=15
+ +
□－□=5
|| ||
3 12
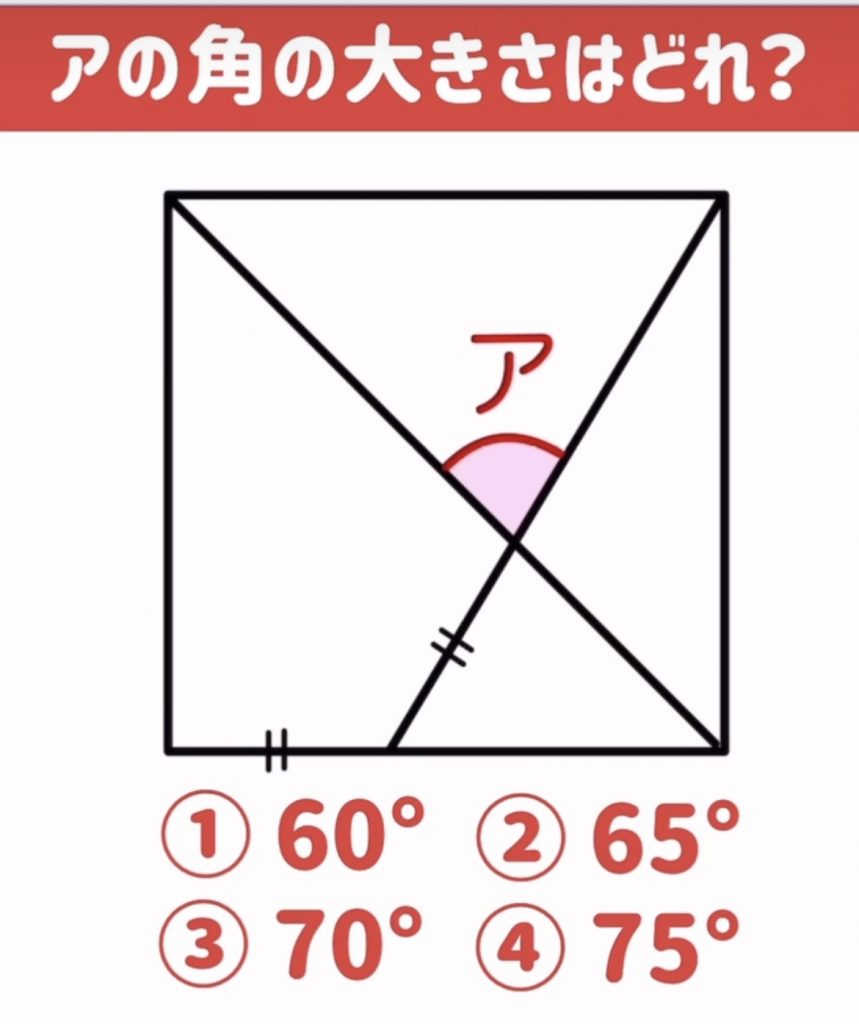
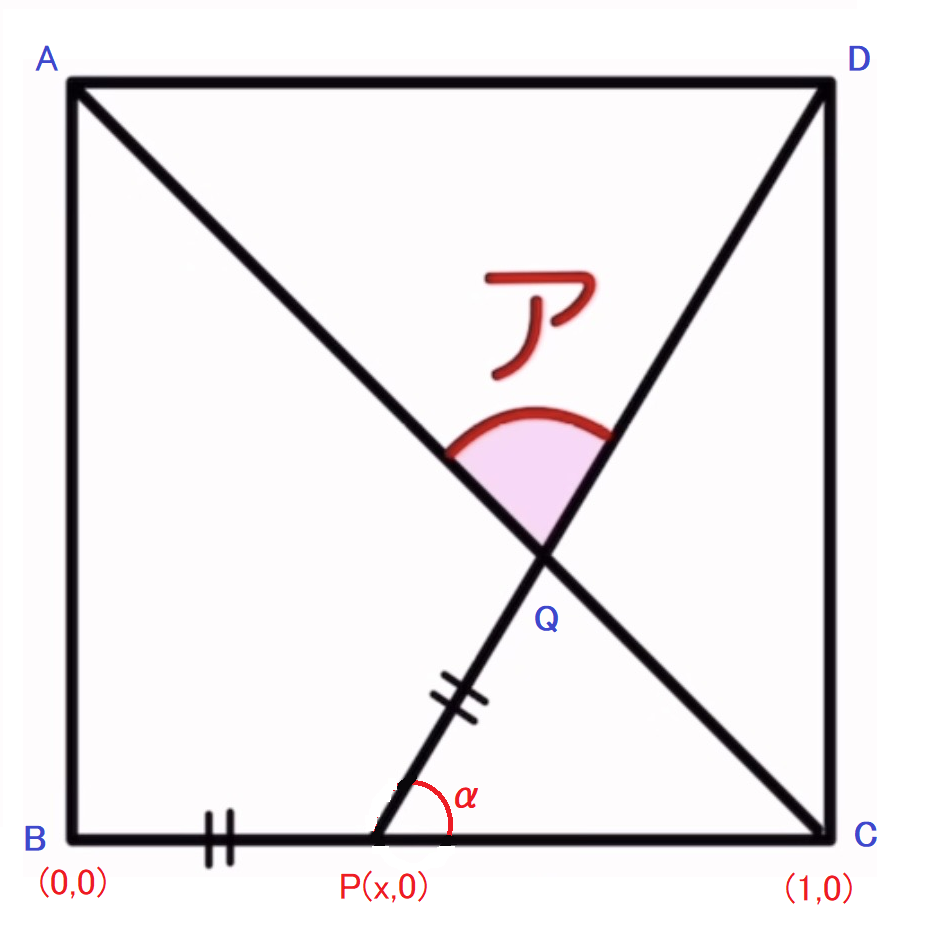
□の中に整数を入れる問題です。未知数が４つで４つの式ができるので連理方程式の問題です。
プログラムで解きました。未知数をa,b,c,dとしてaをー１～15までで条件にあう整数を探しました。
—————————————
for a in range(-15,16):
if a!=0 and 15%a==0:
b=15//a
c=3-a
d=12-b
if c-d==5:
print(a,b,c,d)
結果
-15 -1 18 13
1 15 2 -3
簡単に解けそうな問題である。しかしよく分からない。長さが等しいという線分の長さを求めてみる。
点Pと直線y=-x+1の距離がｘに等しいという式からｘを求める。x=(1-x)/√(2) よりx=√(2) – 1
tan α = 1/PC=1/(2-2√2) より α ≒59.6388
αはほぼ60°になる。
ア≒180-45-60＝75となる。
4択問題なので④を選ぶことになるが正確な値ではない。
算数オリンピック2007 ファイナル問題7
水平な床に長さ2007cm、奥行2cm、高さ2cmの直方体の箱があり、その中を半径1cmの球が転がるようになっています。
箱の丁度中央には球Cがあり、その左に球A、右に球Bがそれぞれ接しています。3つの球の半径は全て1cmです。
いま、球Aが左向きに毎秒7cm、球Bが毎秒37cmの速さで同時に転がり始めました。球Cは静止したままです。
この後、はじめて3つの球が同時に衝するまでの間に球Cは何cmの道のりを転がるか？
ただし各球は何もないところでは等しい速度で真っ直ぐ進み、壁にぶつかると反射して同じ速さで逆向きに進み、球と球が衝突するとそれぞれの速度と向きが相手の球の速度と向きに入れ替わることが知られています。
問題を読むだけでも疲れてしまいます。これは難問です。
これを小学生が解くのは大変です。とりあえず、いつものようにプログラミングで解いてみました。緑のスタートボタンを押してください。
球C（ピンクのボール）が22回の正面衝突をしてその移動距離が22011cmだと分かります。プログラムはこのように球の動作をシミュレートするのは得意です。Scrathはスプライトの衝突を検知するのでプログラムが簡単にできます。さて、この問題を小学生がプログラムも使わずどのように解けばよいのでしょう。
ピンクのボールの動きだけに注目しましょう。規則正しく移動していることが分かります。
長さ2007cmを移動しますが球の半径がすべて1cmです。3つの球の直径を引いてやれば点A,B,Cが移動することになり計算が略になります。
つまり長さを2007-２×３＝2001cmと考えます。ここを点Cが移動する様子をみれば小学生でも移動距離を計算できます。
ネコにタッチすれば求め方を解説してくれます。
中学生以上なら三平方の定理や三角関数を使って一瞬で解く問題かもわかりませんが、これは小学生の問題です。なので三平方の定理や三角関数は使ってはいけません。
この問題を紹介して解答したホームページについて多くのコメントが付いていました。多かったのがECの長さを２として解いている時点で三平方を使っているのではないかというものでした。
また解き方もとても難しくて小学生には無理だという意見が多かったようです。ただ、この図形を4個並べて4倍の正方形の面積を求めるという方法は面白いと感じました。
とりあえず小学生でも解けそうな方法を私なりに考えてみました。
まず、三平方の定理を使わなくてもEC＝２になることを証明しましょう。
三角形CDFは2等辺三角形。
三角形CEFは正三角形なの各辺DF, EF,CF,CEの長さはすべて等しく２になります。
CQは正三角形CEFの垂線なので辺EFを2等分します。だから辺EQの長さは１です。QDの長さは４－１＝３です。
三角形DPCの面積は４×３÷２＝６です。
この三角形の面積は正方形の面積の半分なので正方形の面積は６×２＝１２です。
長針、短針、秒針のついた時計がある。7時から8時までの間で、短針と秒針の間の角度が120°になる23回目の時刻は7時何分何秒か？
面倒な問題です。短針と秒針の角度が120°になるのは1分間に2回あるので23回目は7時11分台の1回目。
7時11分ｘ秒の短針の角度は
\[210＋11×0.５＋\frac{x}{120}\]
秒針のｘ秒後の角度は6xなので
\[210＋11×0.５＋\frac{x}{120}-6x＝120\] となるxを求めればよい。
\[x=\frac{11460}{719}=15×\frac{675}{719}\]
答えは7時11分15.94秒
１から９９９までの整数のうち、約数の個数が5個であるものをすべて求めなさい。
難しい問題です。約数の個数が5個の整数は素数の４乗だということを知っていれば答えは分かります。
素数 素数の４乗
２ ２４＝16
３ ３４＝27
５ ５４＝625
７ ７４＝2401
答えは16,27,625です。
それでは１から９９９までの整数のうち約数の個数が最も多い整数はいくらでしょう？
答え：８４０で約数の個数は32個
栄東中の入試問題
辺ABの中点をP、辺CDの中点をQとします。
PQの長さが6cmのとき、正四面体ABCDの体積は何㎠ですか。
正四面体の各辺の中点を結ぶと正四面体の中に正八面体ができます。
この正八面体の体積を求めます。底面積は対角線の長さが5cmの正方形で高さが6cmなので６×６÷２×6÷3=36㎤です。正四面体の4隅に小さな正四面体が4個できます。小さな正四面体の体積を①とすると大きい正四面体の体積は⑧です。
⑧ー④は正八面体の体積になりますので⑧ー④＝④＝36㎤です。①=９となり小さい正四面体の体積が９㎠だと分かります。
大きい正四面体の体積は小さな正四面体の体積の8倍なので
９×８＝72㎤が答えです。
甲陽学院中の入試問題から
以下のように数が並んでいます。
1行目 1
2行目 3,4,5
3行目 7,8,9,10,11
4行目 13,14,15,16,17,18,19
5行目 21,22,23,24,25,26,27,28,29
：
3600は何行目の何番目の数ですか？
各行の最初の数字は1,3,7,13,21,・・・
この数列の一般項 an=n2-n+1
n=60のときa60=602-60+1=3541
3600-3541+1=60
よって60行目の60番目
これも中学入試の問題です。四角形ABCDは正方形で三角形DEFは１辺の長さが８ｃｍの正三角形です。斜線部分の面積の合計は何㎠ですか。
これは難問です。解答を知るとちょっと感動するかも。
答えは16㎠です。
三角形DGHは30°、60°の角を持つ直角三角形だから
GH=DC÷2＝４(cm)
よって斜辺部分の面積の合計は
８×４÷２＝16（㎠）
中学入試の問題は本当に難しい！
ある池の周りをA君とB君は同じ方向に、C君は逆方向に、それぞれ一定の速さで回ります。A君はB君を15分ごとに追い越し、B君はC君と３分ごとに出会います。
B君が７分かかって回る距離をC君は８分で回ります。
A君とB君とC君の速さの比を求めなさい。［麻布中学校］
池の周囲の長さも分からないし、求めるのは速さの比です。小学生がこんな問題を解けるのでしょうか？
C君とD君は同じ距離を７分と８分で回るので速さの比は8:7です。B君とC君の速さを８と７にしましょう。
B君とC君は３分で出会うので
3×8+3×7=45 つまり池の周囲の長さが45です。
１５分間にA君が回る距離とC君の距離の差は池の周囲の長さになります。A君の速さをAとすれば
A×15-8×15=45
A×15=45+120=165
A=11
よってA:B:C=11:8:7