中学3年生に問題の解き方を尋ねられた。
その問題は「4人でじゃんけんをするときあいこになるパターンは何通りあるか?」というものであった。とりあえず、真面目に数学的に解くことにした。
あいこになる場合は
ぐう、ぐう、ちょき、ぱあ
ぐう、ちょき、ちょき、ぱあ
ぐう、ちょき、ぱあ、ぱあ の3通りである。
ぐうが2個、ちょき、ぱあがそれぞれ1個ずつの組合せは
4C2✕2=6✕2=12通りある。
同様に他の2つの場合も12通りなので12✕3=36通り が答え!
簡単な問題である。
これをプログラムで解いてみよう。
シラミつぶし法でじゃんけんのすべてのパターンをつくってその中からあいこのものだけをカウントする。
Pythonだと
i=1
for w in (‘a’,’b’,’c’):
for x in (‘a’,’b’,’c’):
for y in (‘a’,’b’,’c’):
for z in (‘a’,’b’,’c’):
s= w+x+y+z
if (‘a’ in s) and (‘b’ in s) and (‘c’ in s):
print(i,’:’,s)
i=i+1
出力結果は
1 : aabc
2 : aacb
: abac
: abbc
35 : ccab
36 : ccba
となり36通りであることが分かる。
Scratchで同じようなプログラムを作ると
これも簡単にできる。
しかし、気分を変えてこの問題をモンテカルロ法で解いてみた。
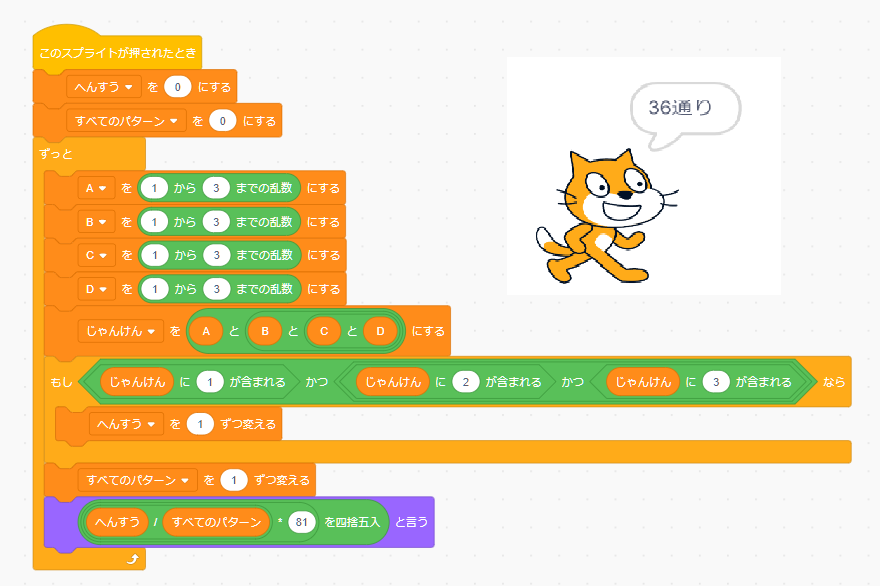
4個の変数をぐう、ちょき、ぱあの乱数にしてあいこだったらカウントするというやり方で求めてみた。
すぐに36通りに収束した。これはモンテカルロ法のよい使用例になったかも。