月: 2023年7月

a₁=1, a_n+1=3a_n – 2ⁿ という漸化式を解け。
累乗が入った漸化式はkⁿを掛けたり割ったりすることで単純な漸化式になることが多い。
両辺を2ⁿ⁺¹で割ると
a_n+1/2ⁿ⁺¹ = 3a_n/(2・2ⁿ) – 1/2
ここでbn=an/2ⁿとおくと、
b_n+1 = 3b_n/2 – 1/2
2b_n+1 = 3b_n – 1
b_n = -(3/2)ⁿ/3+1
a_n = 2ⁿb_n = 2ⁿ – 3^n-1

漸化式から一般項を求めるのはとても難しい。
しかし、実際こんな必要があるのだろうか？
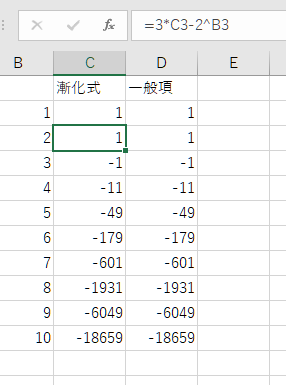
コンピュータを使えば漸化式から簡単に値を求めることができる。
Excelで計算した例であるが、セルC1にa1の値を入れてc2に漸化式の式 [=3*C3-2^B3]を入れて下にコピーするだけで計算できる。
どんな難しい漸化式でも大丈夫。

これで良いのではないか？

a₁=1,a_n+1-a_n=n(n+1)で定義される数列{an}について
a₂₀とS₂₀を求めよ。
a_n=1+1・2+2・3+・・・・+n(n+1)

a_n=1+Σ[k=1..n-1]k²+Σ[k=1..n-1]k
　=1+(n-1)n(2n-1)/6+n(n-1)/2
　=(n³-n+3)/3+1
a₂₀=2661

Sn=(Σ[k=1..n]k³ – Σ[k=1..n]k + 3n)/3
　=[{n(n+1)/2}² – n(n+1)/2 +3n]/3
　=n(n³+2n²-n+10)/12
S₂₀=14650

数列{a_n}は、a₁=1/2, a₂=2, a_n+1×a_n-1=(a_n)2 　(n≧2)を満たしている。このときa_nを求めよ。

a_n+1/a_n=a_n/_an-1より等比数列だと分かる。
a₁=1/2、a₂/a₁=4よりa_nは初項1/2,公比4の等比数列なのでa_n=1/2×4^n-1

数列{a_n}のn項までの和がS_n=n・3ⁿ⁺¹-1で表されるときa₁とn≧2に対する一般項a_nを求めよ。
a₁=S₁=9-1=8
a_n=S_n-S_n-1=n・3ⁿ⁺¹-1-(n-1)3ⁿ=(3n-n+1)3ⁿ=(2n+1)3ⁿ

Sn=4n-a_nが成り立つとき
(1) 初項a₁の値を求めよ。
　S₁=a₁=4-a₁ 2a₁=4 a₁=2
(2) a_n+1をa_nで表せ。
　a_n+1=S_n+1-S_n=4(n+1)-a_n+1-4n+a_n
　a_n+1=a_n/2+2
(3) この数列の一般項を求めよ。
　a_n+1-4=(a_n-4)/2 より{a_n-4}は初項がa₁-4=2-4=-2,
公比が1/2の等比数列
　a_n-4=-2×(1/2)^n-1 より
　a_n=-2×(1/2)^n-1+4

a1=0, a2=3とし、
a_n+1=(4/3)a_n-(1/3)a_n-1 (n=2,3,4,・・・・)とする。
一般項を求めよ。
3(a_n+1-a_n)=a_n-a_n-1
(a_n+1-a_n)=(1/3)(a_n-a_n-1)
これは初項が3, 公比が(1/3)の階差数列なので
n-1
a_n=0+ Σ 3×(1/3)^k-1 =(9/2)(1-3^1-n)
k=1

a₁=1, a_n+1=(8a_n-1)/(25a_n-2) (n=1, 2, 3, 4,・・・)について以下の問いに答えよ。
(1) a₂, a₃, a₄, a₅を求めよ。
a₁=1/2, a₂=2/7, a₃=3/12, a₄=4/17, a₅=5/22
分子はn, 分母は初項2, 公差5の等差数列と予想する。
a_n=n/{2+5(n-1)}=n/(5n-3)
このanをa_n+1=(8a_n-1)/(25a_n-2)に代入する
分子は(8a_n-1)＝(8n-5n+3)/(5n-3)=(3n+3)/(5n-3)
分母は(25n-10+6)/(5n-3)=(15n+6)/(5n-3)
よってa_n+1=(3n+3)/(15n+6)=(n+1)/(5n+2)………①
また、a_n=n/(5n-3)より
a_n+1=(n+1)/{5(n+1)-3}=(n+1)/(5n+2)………②
①=②から予想は正しい。