月: 2023年2月

【例題】 24, 42の最大公約数と最小公倍数を求める。

すだれ法で求めます。
2 ) 24, 42
3 ) 12, 21
　　4, 7
最大公約数=2×3=6
最小公倍数=2×3×4×7=168

ユークリッドの互除法を使います。
42÷24=1・・・18
24÷18=1・・・6
18÷ 6 =3・・・0　余りが０になったら終了
最大公約数は 6
2 数を同時に割れる数がパッと思いつかない場合は、この方法を使います。

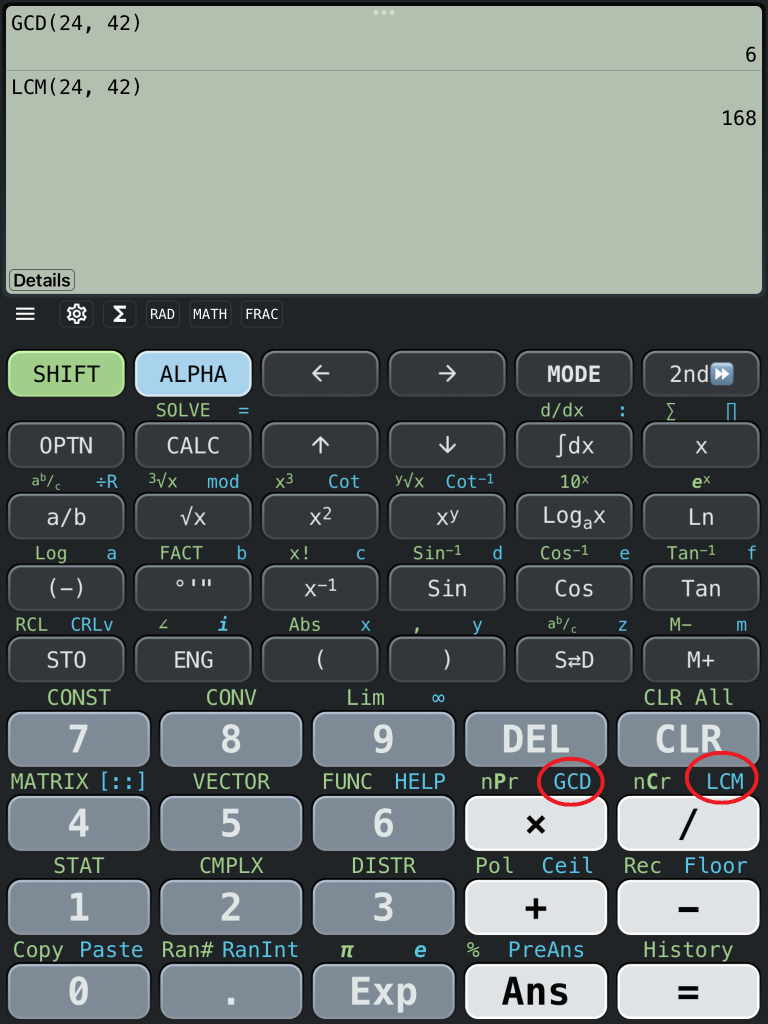
関数電卓を使う。
スマホ用の関数電卓を使って簡単に求めることができます。
関数名のGCD（最大公約数）とLCM（最小公倍数）を見つけます。

【例題】 60,126,450 の場合
最大公約数は
2 ) 60 126 450　
3 ) 30 63 225
　　10 21 75
最大公約数＝２×３＝６

最小公倍数は
2) 60 126 450
3) 30 63 225
3) 10 21 75　←　割り切れない数字はそのまま下に書く
5) 10 7 25
　　2 7 5
最小公倍数＝ 2²×3²×5²×7＝6300

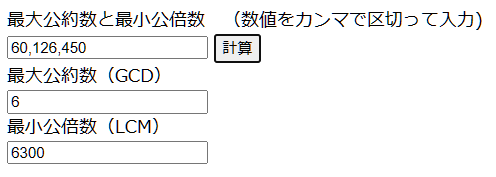
ホームページの利用

【例題】nと36の最小公倍数が504になるようなｎをすべて求めよ。次数が小さければ大きい方を選ぶ。同じなら次数が０～その次数までを選ぶ。なければその数字を選びすべてを掛ける。
504=2³×3²×7
36=2²×3²
n=2³ ×(3⁰or3¹or3²)×7=56, 168, 504

【例題】nと48の最小公倍数が720になるようなｎをすべて求めよ。
720=2⁴×3²×5
48=2⁴×3
n=(2⁰or2¹or2²or2³or2⁴)×3²×5=45, 90, 180, 360, 720

ずっと愛用していたいPhone8からiPhone12に変更しました。
新しい機種なので性能はアップしたけどまだ使い方になれなくて苦労しています。