令和５年度 本試験の正解
数Ⅰ・A 本試験の正解
数Ⅱ・B 本試験の正解
令和５年度 追・再試験の正解
令和５年度 数Ⅰ・A 追・再試験の正解
令和５年度 数Ⅱ・B 追・再試験の正解
共通テストの自己採点ツール
共通テストの過去問題
月: 2023年1月
カテゴリー
余りを求める問題
20232023を11で割った余りはいくらか？
2023２を11で割ると余りが1になる。
20232023=(20232)1011✕2023≡2023≡10 (mod 11)
よって余りは10である。
しかしプログラムを使えば１行で答えが求まる。
print(2023**2023%11)
カテゴリー
保護中: 碁石の問題
カテゴリー
平方数列の和を求める
平方数列の和というのは
12+22+32+42+52+・・・・+n2
ガウスは小学生の時に1+2+3+・・・・nを求めたのでもうすこし難しい問題に挑戦！
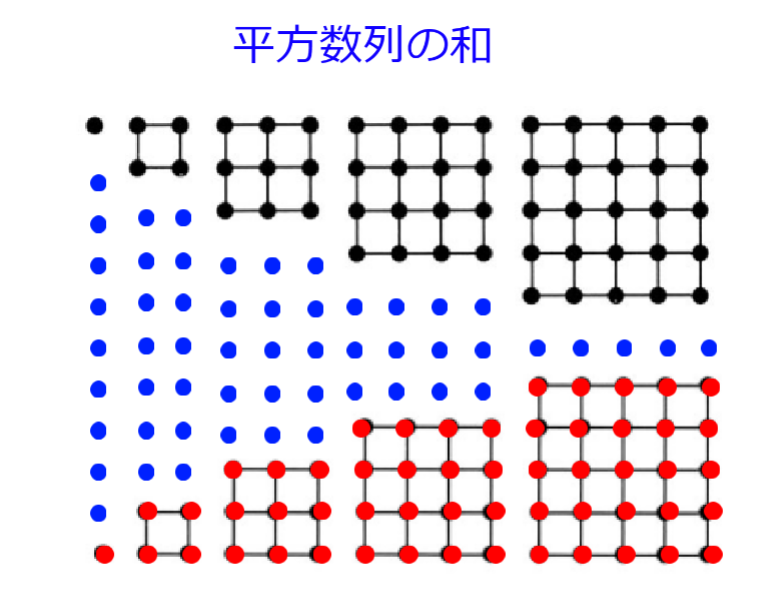
図はn=5のときに様子で赤丸の数が平方数列の和になる。
黒丸と青丸は同じ数の丸でこのように並べると長方形になる。
縦はn+2で横は1+2+3+・・・+nでガウスが求めた数
n(n+1)/2になる。
そこで平方数列の和はn(n+1)(n+2)/2÷3で求められる。
つまり平方数列の和
中村儀作・阿邊恵一著「代数を図形で解く」を参考にしました。
カテゴリー
フェルマー数
Fn＝２２＾ｎ＋1 (nは自然数, 2^nは2n）
F0＝3
F1＝5
F2＝17
F3＝257
F4＝65537
F0からF4はすべて素数です。
フェルマーはF5=4294967297も素数だろうと予想しました。フェルマーから約百年後、1732年にオイラーはフェルマーの予想が誤りであったことを示しました。
F5が素数でないことは簡単に示せます。
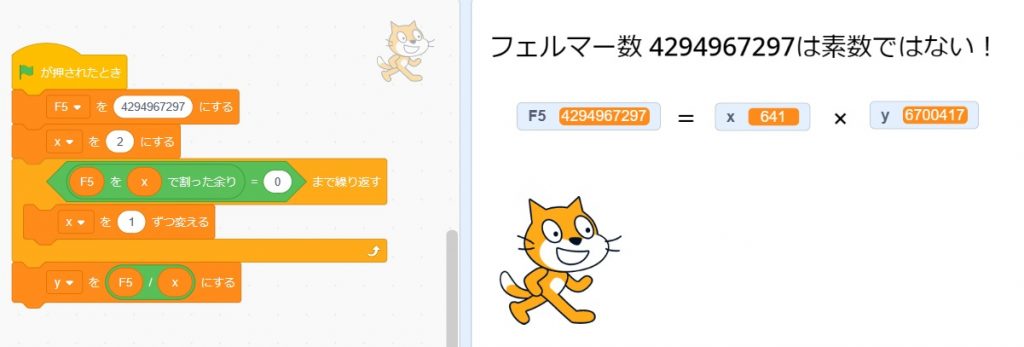
F6はScratchでは難しいのでPythonで解きました。
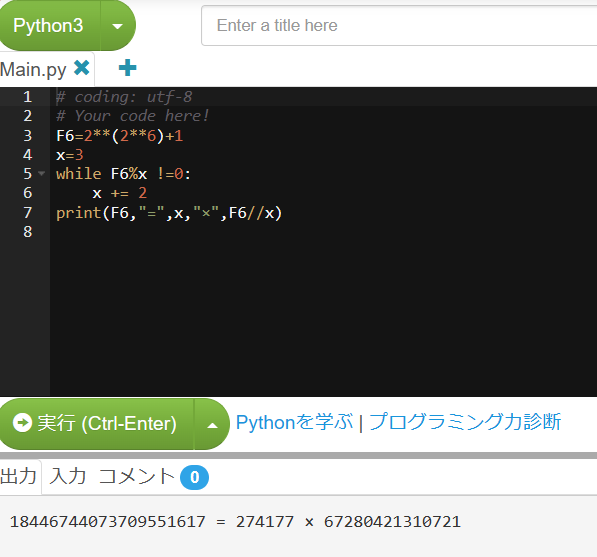
Pythonだと簡単に素因数分解できました。これでF6は素数でないことが分かります。
フェルマーの予想から百年後にオイラーがF5が誤りであることを示しましたがそれから150年近くたった1880年にランドリーによって素因数分解されました。驚くことに80歳を過ぎてからの大発見だったそうです。
その後コンピュータを使ってF7,F8,F11が素因数分解できることが解き明かされています。
この記事は「面白くて眠れなくなる数学」桜井進著を参考にしました。
余談ですが、F7の値が初版では間違っていました。