栄東中の入試問題
辺ABの中点をP、辺CDの中点をQとします。
PQの長さが6cmのとき、正四面体ABCDの体積は何㎠ですか。
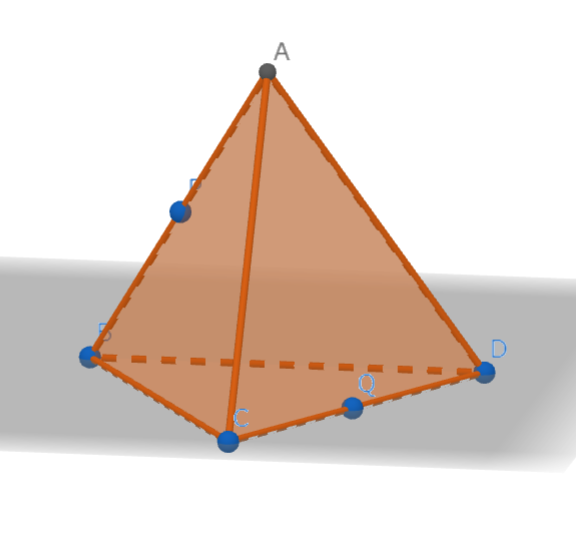
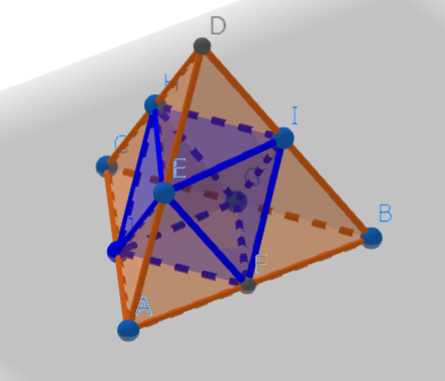
正四面体の各辺の中点を結ぶと正四面体の中に正八面体ができます。
この正八面体の体積を求めます。底面積は対角線の長さが5cmの正方形で高さが6cmなので6×6÷2×6÷3=36㎤です。正四面体の4隅に小さな正四面体が4個できます。小さな正四面体の体積を①とすると大きい正四面体の体積は⑧です。
⑧ー④は正八面体の体積になりますので⑧ー④=④=36㎤です。①=9となり小さい正四面体の体積が9㎠だと分かります。
大きい正四面体の体積は小さな正四面体の体積の8倍なので
9×8=72㎤が答えです。