中学生以上なら三平方の定理や三角関数を使って一瞬で解く問題かもわかりませんが、これは小学生の問題です。なので三平方の定理や三角関数は使ってはいけません。
この問題を紹介して解答したホームページについて多くのコメントが付いていました。多かったのがECの長さを2として解いている時点で三平方を使っているのではないかというものでした。
また解き方もとても難しくて小学生には無理だという意見が多かったようです。ただ、この図形を4個並べて4倍の正方形の面積を求めるという方法は面白いと感じました。
とりあえず小学生でも解けそうな方法を私なりに考えてみました。

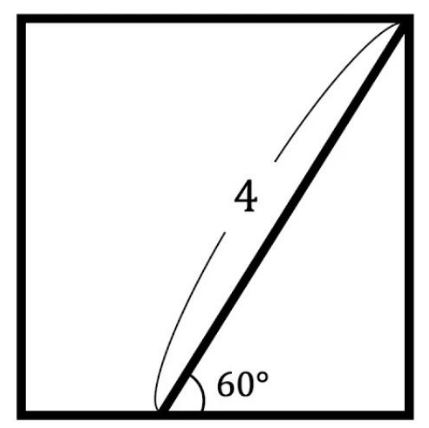
まず、三平方の定理を使わなくてもEC=2になることを証明しましょう。
三角形CDFは2等辺三角形。
三角形CEFは正三角形なの各辺DF, EF,CF,CEの長さはすべて等しく2になります。
CQは正三角形CEFの垂線なので辺EFを2等分します。だから辺EQの長さは1です。QDの長さは4-1=3です。
三角形DPCの面積は4×3÷2=6です。
この三角形の面積は正方形の面積の半分なので正方形の面積は6×2=12です。