因数分解の問題

ネットでこのような問題が紹介されていました。
x¹⁴+x⁷+1を係数が実数の範囲で因数分解せよ。
簡単そうに見えます。しかし、これは数学検定１級の問題でしかも解答が間違っていたという有名な難問だそうです。
日本の数学は因数分解の勉強にすごく時間をかけていると言われていますが、確かにそうだと思います。
実際に解いてみました。
とりあえずf(x)=x¹⁴+x⁷+1がどんなグラフになるのかを見てみましょう。グラフはパソコンやスマホで簡単に表示できます。

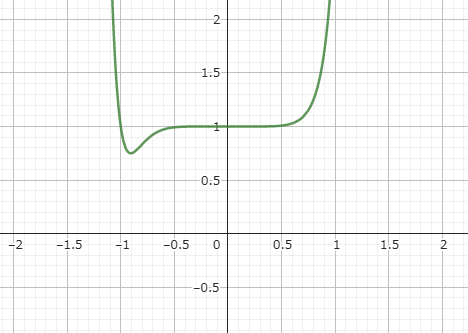
x軸とは交わらないのでf(x)=0となるxは虚数になることが分かります。つまり因数定理なんかでは因数分解できない。
それならx7=Xとすればこの式はX²+X+1になります。
X²+X+1=0となるXは解の公式よりX=(-2±i√(3))/2
この値をxとしてf(x)に代入するとf((-2±i√(3))/2)=0となることからf(x)は(x²+x+1)で因数分解できることが分かります。
早速　(x¹⁴+x⁷+1)÷(x²+x+1)を筆算で計算すると
f(x)=(x²+x+1)(x¹²-x¹¹+x⁹-x⁸+x⁶-x⁴+x³-x+1)
これでとりあえず因数分解できました。
「係数が整数の範囲で因数分解せよ」というのならこれで正解です。
しかし「係数が実数の範囲で因数分解せよ」というのだからさらにこれは因数分解できます。